题目内容
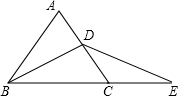
 如图,在直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△ABO,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.下列结论正确的有( )个:
如图,在直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△ABO,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.下列结论正确的有( )个:(1)△OBC≌△ABD;
(2)点E的位置不随着点C位置的变化而变化,点E的坐标是(0,
| 3 |
(3)∠DAC的度数随着点C位置的变化而改变;
(4)当点C的坐标为(m,0)(m>1)时,四边形ABDC的面积S与m的函数关系式为S=
| ||
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:全等三角形的判定与性质,坐标与图形性质,等边三角形的性质
专题:动点型
分析:(1)易证∠OBC=∠ABD,即可证明△OBC≌△ABD,即可解题;
(2)根据(1)容易得到∠OAE=60°,然后在中根据直角三角形30°,所对的直角边等于斜边的一半可以得到AE=2,从而得到E的坐标是固定的.
(3)根据∠OAE=60°可得∠DAC=60°,可得∠DAC的度数不会随着点C位置的变化而改变;即可证明该结论错误;
(4)根据△OBC≌△ABD,可得四边形ABDC的面积S=S△ACD+S△ABD=S△ACD+S△OBC,即可解题.
(2)根据(1)容易得到∠OAE=60°,然后在中根据直角三角形30°,所对的直角边等于斜边的一半可以得到AE=2,从而得到E的坐标是固定的.
(3)根据∠OAE=60°可得∠DAC=60°,可得∠DAC的度数不会随着点C位置的变化而改变;即可证明该结论错误;
(4)根据△OBC≌△ABD,可得四边形ABDC的面积S=S△ACD+S△ABD=S△ACD+S△OBC,即可解题.
解答:解:(1)∵△AOB是等边三角形,
∴OB=AB,∠OBA=∠OAB=60°,
又∵△CBD是等边三角形
∴BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
在△OBC和△ABD中,
,
∴△OBC≌△ABD(SAS);(1)正确;
(2)∵△OBC≌△ABD,
∵∠BAD=∠BOC=60°,
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°,
∴Rt△OEA中,
∵∠OAE=60°,
∴∠AEO=30°,
∴AE=2OA=2,
∴OE=
=
,
∴点E的位置不会发生变化,E的坐标为E(0,
);(2)正确;
(3)∵∠OAE=60°,
∴∠DAC=60°,
∴∠DAC的度数不会随着点C位置的变化而改变;(3)错误;
(4)∵△OBC≌△ABD,
∴四边形ABDC的面积S=S△ACD+S△ABD=S△ACD+S△OBC
=
AC•ADsin∠DAC+
OB•OCsin∠BOC
=
×(m-1)m×
+
×1×m×
=
m2,故(4)正确;
故选.
∴OB=AB,∠OBA=∠OAB=60°,
又∵△CBD是等边三角形
∴BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
在△OBC和△ABD中,
|
∴△OBC≌△ABD(SAS);(1)正确;
(2)∵△OBC≌△ABD,
∵∠BAD=∠BOC=60°,
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°,
∴Rt△OEA中,
∵∠OAE=60°,
∴∠AEO=30°,
∴AE=2OA=2,
∴OE=
| 22-12 |
| 3 |
∴点E的位置不会发生变化,E的坐标为E(0,
| 3 |
(3)∵∠OAE=60°,
∴∠DAC=60°,
∴∠DAC的度数不会随着点C位置的变化而改变;(3)错误;
(4)∵△OBC≌△ABD,
∴四边形ABDC的面积S=S△ACD+S△ABD=S△ACD+S△OBC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 4 |
故选.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、面积相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△OBC≌△ABD是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
抛物线y=2(x+3)2+1的顶点坐标是( )
| A、(3,1) |
| B、(3,-1) |
| C、(-3,1) |
| D、(-3,-1) |
单项式-3a2b的次数为( )
| A、1 | B、2 | C、3 | D、-3 |
下列是一元一次方程的是( )
| A、x2-4=0 | ||
| B、x+y=3 | ||
C、
| ||
| D、5x=1 |

 如图,在等边△ABC中,BD平分∠ABC,延长BC到点E,使CE=CD,连接DE.
如图,在等边△ABC中,BD平分∠ABC,延长BC到点E,使CE=CD,连接DE. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC=
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC=