题目内容
1.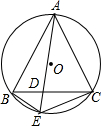 如图,已知△ABC为⊙O的内接三角形,AB=AC=5,AD=4,则DE的长为$\frac{9}{4}$.
如图,已知△ABC为⊙O的内接三角形,AB=AC=5,AD=4,则DE的长为$\frac{9}{4}$.
分析 由已知条件和圆周角定理易证△ABD∽△AEB,由相似三角形的性质:对应边的比值相等可得AB,AD,AE的之间的数量关系,结合图形可得AE=AD+DE,进而可求出DE的长.
解答 解:
∵AB=AC=5,
∴∠ABD=∠ACB,
∵∠ACB=∠AEB,
∴∠ABD=∠AEB,
∵∠BAE=∠BAE,
∴△ABD∽△AEB,
∴$\frac{AB}{AD}=\frac{AE}{AB}$,
即AB2=AD•AE,
∵AD=4,AE=AD+DE,
∴52=4•(4+DE),
解得DE=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题主要考查了三角形外接圆与外心的有关性质,用到的知识点有等腰三角形的性质、圆周角定理以及相似三角形的判定与性质,能够判定△ABD∽△AEB是解题的关键.

练习册系列答案
相关题目
11.取15张扑克牌,其中6张“方块”,3张“梅花”,6张“红桃”,从中任抽一张,是“方块”或“红桃”的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
20.若a-5>b-5,则下列式子错误的是( )
| A. | a>b | B. | -$\frac{1}{2}$a<-$\frac{1}{2}$b | C. | 2a+3>2b+3 | D. | -7a>-7b |
 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.
如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.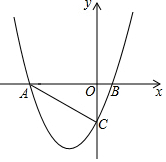 如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.
如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.