题目内容
请借助数轴求解:甲、乙两人分别开车从武汉出发到某风景区游玩,途中要经过一个高速公路收费站和一个休息站.当乙到达收费站时,甲才出发;当甲经过收费站半小时后得知乙已经到达休息站,此时乙已经走了全程的
;当甲到达休息站时,乙离风景区只有
的路程.已知甲、乙两车始终保持60千米/时的速度行驶,途中也没有休息,问甲比乙晚出发多长时间?
| 1 |
| 2 |
| 1 |
| 3 |
考点:三元一次方程组的应用
专题:
分析:假设收费站离休息站距离B千米、休息站离终点距离2A千米、起点到收费站距离C千米,根据根据“乙到达收费站时,甲才出发;当甲经过收费站半小时后得知乙已经到达休息站”,可得(B-C)=60×0.5=30,由于C+B=A,根据“当甲到达休息站时,乙离风景区只有
的路程”,可得B-30=A-
A,联立可得A,B,C的值,进一步即可求解.
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:如图:

设收费站离休息站距离B千米、休息站离终点距离2A千米、起点到收费站距离C千米;
根据“乙到达收费站时,甲才出发;当甲经过收费站半小时后得知乙已经到达休息站”
可得(B-C)=60×0.5=30,
C=B-30,
∵C+B=A,
∴2B-30=A,
根据“当甲到达休息站时,乙离风景区只有1/3的路程”
可得B-30=A-
A=
A=
(2B-30),
3B-90=2B-30,
B=60,
A=90,
C=A-B=90-60=30,
甲比乙晚出发时间=
=0.5(小时).
答:甲比乙晚出发0.5小时.

设收费站离休息站距离B千米、休息站离终点距离2A千米、起点到收费站距离C千米;
根据“乙到达收费站时,甲才出发;当甲经过收费站半小时后得知乙已经到达休息站”
可得(B-C)=60×0.5=30,
C=B-30,
∵C+B=A,
∴2B-30=A,
根据“当甲到达休息站时,乙离风景区只有1/3的路程”
可得B-30=A-
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
3B-90=2B-30,
B=60,
A=90,
C=A-B=90-60=30,
甲比乙晚出发时间=
| 30 |
| 60 |
答:甲比乙晚出发0.5小时.
点评:考查了三元一次方程组的应用,解答此类题目的关键是画出数轴,根据数形结合解题.

练习册系列答案
相关题目
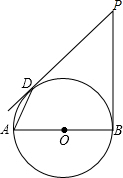 已知:PB切⊙O于B,AB为⊙O的直径,PO∥AD,求证:PD为⊙O的切线.
已知:PB切⊙O于B,AB为⊙O的直径,PO∥AD,求证:PD为⊙O的切线. 按要求作图:平面上有A,B,C三点,如图所示,画直线AC,射线BC,线段AB,在射线BC上取点D,使BD=AB.
按要求作图:平面上有A,B,C三点,如图所示,画直线AC,射线BC,线段AB,在射线BC上取点D,使BD=AB. 如图所示,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角?
如图所示,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角? 如图,已知正方形ABCD中,点E为BC边上一点,BE=1,tan∠BAE=
如图,已知正方形ABCD中,点E为BC边上一点,BE=1,tan∠BAE=