题目内容
1.某汽车租赁公司要购买轿车和面包车共10辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元(1)求最多购买轿车多少辆?
(2)若购买的面包车多于购买轿车的2倍,求至少购买面包车多少辆?
分析 (1)设购买轿车x辆,根据公司可投入的购车款不超过55万元可列不等式求解;
(2)设购买面包车y辆,根据购买的面包车多于购买轿车的2倍可列不等式求解.
解答 解:(1)设购买轿车x辆,则购买面包车(10-x)辆,
根据题意得:7x+4(10-x)≤55,
解得:x≤5.
答:最多购买轿车5辆.
(2)设购买面包车y辆,则购买轿车(10-y)辆,
根据题意得:y>2(10-y),
解得:y>$\frac{20}{3}$,
∵y为整数,
∴y≥7.
答:至少购买面包车7辆.
点评 本题考查一元一次不等式的应用和理解题意的能力,关键是以轿车和面包车的数量关系做为不等量关系,以及购车款做为不等量关系列不等式求解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
9.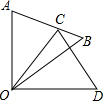 如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,那么∠BOC的度数为( )
如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,那么∠BOC的度数为( )
 如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,那么∠BOC的度数为( )
如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,那么∠BOC的度数为( )| A. | 12° | B. | 14° | C. | 24° | D. | 30° |
16.下列各式从左到右的变形中,为因式分解的是( )
| A. | y2-1=(y+1)(y-1) | B. | x•(a-b)=ax-bx | ||
| C. | x2-1+y2=(x-1)(x+1)+y2 | D. | ax+by+c=x(a+b)+c |
6.平行四边形的一个角比它的邻角的2倍还大15°,则相邻两个角为( )
| A. | 30°,75° | B. | 40°,95° | C. | 50°,115° | D. | 55°,125° |
13.如果P(m,1-3m)在第四象限,那么m的取值范围是( )
| A. | 0<m<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<m<0 | C. | m<0 | D. | m>$\frac{1}{3}$ |
 如图,在?ABCD中,∠B=60°,点E、F分别是边BC、AB上的点,且DF垂直平分AE,若BF=1,且EF⊥AB,则线段AD的长为$\sqrt{3}+$3.
如图,在?ABCD中,∠B=60°,点E、F分别是边BC、AB上的点,且DF垂直平分AE,若BF=1,且EF⊥AB,则线段AD的长为$\sqrt{3}+$3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,现有以下几个方案:
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,现有以下几个方案: 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论: