题目内容
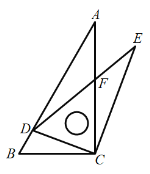
【题目】已知圆![]() 是等边
是等边![]() 的外接圆,延长
的外接圆,延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() 交圆
交圆![]() 于
于![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() ,延长
,延长![]() 至交
至交![]() 于
于![]() .
.
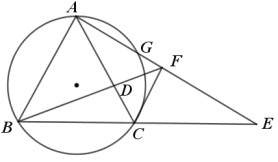
(1)求证:![]() ;
;
(2)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(3)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)2
【解析】
(1)根据等边三角形的性质可得AC=BC,∠ACB=∠BAC=∠ABC=60°,根据![]() 作等量代换进而可得
作等量代换进而可得![]() ,再结合∠BAC=60°即可得证;
,再结合∠BAC=60°即可得证;
(2)过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,OA,先证
,OA,先证![]() ≌
≌![]() ,可得
,可得![]() ,进而根据等腰三角形的三线合一可得
,进而根据等腰三角形的三线合一可得![]() ,再证得
,再证得![]() 即可得证;
即可得证;
(3)连接![]() ,先证明
,先证明![]() ,再根据
,再根据![]() 可得
可得![]() ,进而可得答案.
,进而可得答案.
(1)证明:![]() 是等边三角形,
是等边三角形,
∴AC=BC,∠ACB=∠BAC=∠ABC=60°,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ;
;
(2)证明:如图,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,OA,
,OA,
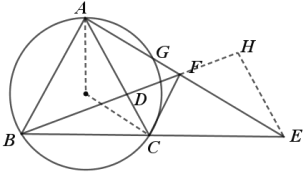
![]() 是
是![]() 的中点,
的中点,
∴由三角形中位线的性质知![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,CF⊥
,CF⊥![]() ,
,
∵∠ABC=60°,
∴∠AOC=2∠ABC=120°,
∵OA=OC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是圆
是圆![]() 的切线;
的切线;
(3)如图,连接![]() ,
,
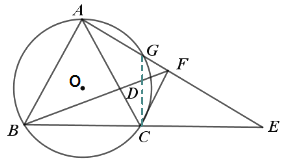
∵∠ABC+∠AGC=180°,∠CGF+∠AGC=180°,
∴![]() ,
,
∵CF⊥![]() ,
,
∴∠CFG=90°,
∴![]()
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△CGF中,![]() ,
,
∴![]() ,
,
∴![]()

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目