题目内容
3.任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)=$\frac{n}{m}$.如:12=1×12=2×6=3×4,则F(12)=$\frac{4}{3}$.则在以下结论:①F(5)=5;②F(24)=$\frac{8}{3}$; ③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.则正确的结论有①③(填序号)
分析 根据最佳分解的定义逐条分析四条结论,找出数的因数找出最佳分解,由此即可得出结论.
解答 解:①5=1×5,F(5)=$\frac{5}{1}$=5,
∴①正确;
②24=1×24=2×12=3×8=4×6,F(24)=$\frac{6}{4}$=$\frac{3}{2}$,
∴②错误;
③a=1×a=$\sqrt{a}$•$\sqrt{a}$,F(a)=$\frac{\sqrt{a}}{\sqrt{a}}$=1,
∴③正确;
④当x=4时,a=x3=64,
∵64=1×64=2×32=4×16=8×8,F(64)=$\frac{8}{8}$=1,
∴④错误.
故答案为:①③.
点评 本题考查了因式分解的应用,解题的关键是逐条分析四条结论.本题属于基础题,难度不大,解决该题型题目时,找出各数的最佳分解是关键.

练习册系列答案
相关题目
15.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2016年5月1日起对居民生活用电试行新的“阶梯电价”收费,具体收费标准如表:
2016年5月份,该市居民甲用电200千瓦时,交费170元;居民乙用电400千瓦时,交费400元.
(1)求上表中a、b的值:
(2)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价每千瓦时不超过0.85元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
| 不超过150千瓦时的部分 | a |
| 超过150千瓦时,但不超过300千瓦时的部分 | b |
| 超过300千瓦时的部分 | a+0.5 |
(1)求上表中a、b的值:
(2)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价每千瓦时不超过0.85元?
 如图,在平面直角坐标系中,AM、DM分别平分∠BAC,∠ODE,且∠MDO-∠MAC=45°,AB交y轴于F:
如图,在平面直角坐标系中,AM、DM分别平分∠BAC,∠ODE,且∠MDO-∠MAC=45°,AB交y轴于F: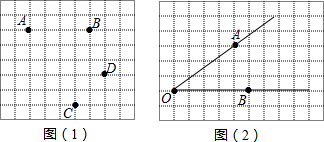
 如图,∠1与∠2互为补角,∠3=120°,求∠4的度数.
如图,∠1与∠2互为补角,∠3=120°,求∠4的度数.
 如图,Rt△ABC中,∠ABC=90°,tan∠CAB=2,点D为BC中点,连接AD,BE⊥AC于E,交AD于点G.DF⊥AD交AC于F,若DF=5,则DG=$\frac{10}{3}\sqrt{10}$..
如图,Rt△ABC中,∠ABC=90°,tan∠CAB=2,点D为BC中点,连接AD,BE⊥AC于E,交AD于点G.DF⊥AD交AC于F,若DF=5,则DG=$\frac{10}{3}\sqrt{10}$..