题目内容
4.解下列方程组:(1)$\left\{\begin{array}{l}{y=2x-3}\\{4x-3y=1}\end{array}\right.$.
(2)$\left\{{\begin{array}{l}{x+2y-z=6}\\{2x+y+z=9}\\{3x+4y+z=18}\end{array}}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{y=2x-3①}\\{4x-3y=1②}\end{array}\right.$,
把①代入②得:4x-3(2x-3)=1,
解得:x=4,
把x=4代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+2y-z=6①}\\{2x+y+z=9②}\\{3x+4y+z=18③}\end{array}\right.$,
①+②得:x+y=5④,
①+③得:2x+3y=12⑤,
⑤-④×2得:y=2,
把y=2代入④得:x=3,
把x=3,y=2代入①得:z=1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
12.一鞋店试销一种新款女鞋,一周内各种型号的鞋卖出的情况如下表所示:
对该鞋店的经理来说,他最关注的是鞋的销售量这组数据的( )
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量(双) | 4 | 6 | 11 | 17 | 8 | 5 | 3 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
9.下列计算正确的是( )
| A. | x3+x2=x5 | B. | x4÷x=x4 | C. | (x3)2=x5 | D. | x3•x2=x5 |
16.若(a-2y)(y-1)的结果不含y的一次项,则( )
| A. | a=1 | B. | a=-1 | C. | a=2 | D. | a=-2 |
 如图,将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形.若灰色长方形的长与宽之比为5:3,则AD:AB=47:29.
如图,将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形.若灰色长方形的长与宽之比为5:3,则AD:AB=47:29.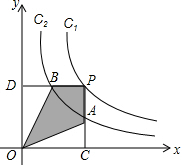 如图,两个反比例函数y=$\frac{5}{x}$和y=$\frac{k}{x}$在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图,两个反比例函数y=$\frac{5}{x}$和y=$\frac{k}{x}$在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )