题目内容
13. 在平行四边形DECF中,B是CE延长线上一点,A是CF延长线上一点,连接AB恰过点D,求证:AD•BE=DB•EC.
在平行四边形DECF中,B是CE延长线上一点,A是CF延长线上一点,连接AB恰过点D,求证:AD•BE=DB•EC.
分析 由四边形DECF是平行四边形知DE∥AC、DF∥BC且DF=EC,从而得∠ADF=∠B、∠A=∠BDE,即可证△ADF∽△DBE得$\frac{AD}{DB}$=$\frac{DF}{BE}$,可得答案.
解答 证明:∵四边形DECF是平行四边形,
∴DE∥AC、DF∥BC,且DF=EC,
∴∠ADF=∠B、∠A=∠BDE,
∴△ADF∽△DBE,
∴$\frac{AD}{DB}$=$\frac{DF}{BE}$,
∵DF=EC,
∴$\frac{AD}{DB}$=$\frac{EC}{BE}$,即AD•BE=DB•EC.
点评 本题主要考查平行四边形的判定与性质及平行四边形的性质,熟练掌握平行四边形的对边平行且相等是证明相似的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.国家统计局的相关数据显示,2015年我国国民生产总值(GDP)约为67670000000000元,将67670000000000用科学记数法表示为( )
| A. | 6.767×1013 | B. | 6.767×1012 | C. | 67.67×1012 | D. | 6.767×1014 |
 一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )
一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( ) 如图,在边长为1的小正反形组成的网格中,△ABC的三个顶点均在格点上,则tanB的值为$\frac{3}{4}$.
如图,在边长为1的小正反形组成的网格中,△ABC的三个顶点均在格点上,则tanB的值为$\frac{3}{4}$. 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.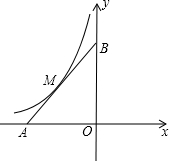 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-$\frac{9}{x}$的图象与线段AB交于M点,且AM=BM.
已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-$\frac{9}{x}$的图象与线段AB交于M点,且AM=BM.