题目内容
 将下面的证明过程补充完整,括号内写上相应理由或依据:
将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠B+∠BDG=180°,试说明∠BEF=∠CDG.
证明:∵CD⊥AB,EF⊥AB(已知)
∴∠BFE=∠BDC=90°(
∴EF∥
∴∠BEF=
又∵∠B+∠BDG=180°(已知)
∴BC∥
∴∠CDG=
∴∠CDG=∠BEF(
考点:平行线的判定与性质
专题:推理填空题
分析:根据垂直定义和平行线的判定推出EF∥CD,推出∠BEF=∠BCD,根据平行线的判定推出BC∥DG,根据平行线的性质得出∠CDG=∠BCD即可.
解答:证明:∵CD⊥AB,EF⊥AB(已知),
∴∠BFE=∠BDC=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠BEF=∠BCD(两直线平行,同位角相等),
又∵∠B+∠BDG=180°(已知)
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠CDG=∠BEF(等量代换),
故答案为:垂直定义,CD,同位角相等,两直线平行,∠BCD,
两直线平行,同位角相等,DG,同旁内角互补,两直线平行,∠BCD,两直线平行,内错角相等,等量代换.
∴∠BFE=∠BDC=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠BEF=∠BCD(两直线平行,同位角相等),
又∵∠B+∠BDG=180°(已知)
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠CDG=∠BEF(等量代换),
故答案为:垂直定义,CD,同位角相等,两直线平行,∠BCD,
两直线平行,同位角相等,DG,同旁内角互补,两直线平行,∠BCD,两直线平行,内错角相等,等量代换.
点评:本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
 如图,水平放置的空心圆柱体的主视图为( )
如图,水平放置的空心圆柱体的主视图为( )A、 |
B、 |
C、 |
D、 |
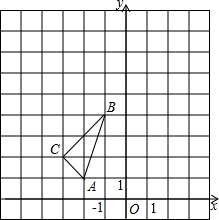 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).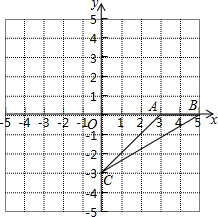 在平面直角坐标系中,△ABC的顶点坐标是A(3,0),B(5,0),C(0,-3).点P(m,n)为△ABC内一点,平移△ABC到△A1B1C1,使点P(m,n)移到点P1(m-4,n+2)处.
在平面直角坐标系中,△ABC的顶点坐标是A(3,0),B(5,0),C(0,-3).点P(m,n)为△ABC内一点,平移△ABC到△A1B1C1,使点P(m,n)移到点P1(m-4,n+2)处.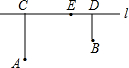 如图,在铁路L的同侧有A、B两村庄,已知A庄到L的距离AC=15km,B庄到L的距离BO=l0km,CD=25km.现要在铁路L上建一个土特产收购站E,使得A、B两村庄到E站的距离相等,
如图,在铁路L的同侧有A、B两村庄,已知A庄到L的距离AC=15km,B庄到L的距离BO=l0km,CD=25km.现要在铁路L上建一个土特产收购站E,使得A、B两村庄到E站的距离相等,
 某市对在当地召开的一个大型国际展览会开幕后连续八天的每日参观人数做了一项调查,并将相关数据绘制成了如下的统计图.请根据所给信息解决下列问题:
某市对在当地召开的一个大型国际展览会开幕后连续八天的每日参观人数做了一项调查,并将相关数据绘制成了如下的统计图.请根据所给信息解决下列问题: 如图,在△ABC中,点E,F分别是AB,AC的中点且EF=1,则BC=
如图,在△ABC中,点E,F分别是AB,AC的中点且EF=1,则BC=