题目内容
1. 如图,矩形OABC在平面直角坐标系中,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-$\frac{3}{4}$x与BC边相交于D点,过原点的抛物线y=ax2+bx经过A、D两点.
如图,矩形OABC在平面直角坐标系中,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-$\frac{3}{4}$x与BC边相交于D点,过原点的抛物线y=ax2+bx经过A、D两点.(1)求抛物线的解析式,并写出对称轴;
(2)试判断△OCD与△ABD是否相似?并说明理由.
(3)在抛物线对称轴上是否存在一点P,使得△POD为直角三角形?若存在,直接写出点P的坐标(并在“备用图”中画出P点得到的痕迹);若不存在,请说明理由.
分析 (1)根据矩形的性质得到OA∥BC,得到D点的纵坐标为-3,求得D(4,-3),把A(6,0),D(4,-3)代入y=ax2+bx即可得到结论;
(2)根据已知条件即可得到结论;
(3)设P(3,m),根据勾股定理得到OP2=9+m2,PD2=(4-3)2+(-3-m)2=m2+6m+10,OD2=32+42=25,列方程即可得到结论.
解答 解:(1)∵四边形OABC是矩形,
∴OA∥BC,
∵C(0,-3),
∴D点的纵坐标为-3,
∵直线y=-$\frac{3}{4}$x与BC边相交于D点,
∴D(4,-3),
把A(6,0),D(4,-3)代入y=ax2+bx得,$\left\{\begin{array}{l}{36a+6b=0}\\{16a+4b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{8}}\\{b=-\frac{9}{4}}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{3}{8}$x2-$\frac{9}{4}$x,其对称轴为直线x=3;
(2)∵OC=3,CD=4,
∴AB=OC=3,BD=2,
∵$\frac{OC}{CD}=\frac{3}{4}$,$\frac{BD}{AB}$=$\frac{2}{3}$,
∴$\frac{OC}{CD}≠\frac{BD}{AB}$,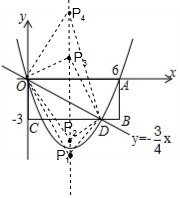
∴△OCD与△ABD不相似;
(3)设P(3,m),
∴OP2=9+m2,PD2=(4-3)2+(-3-m)2=m2+6m+10,OD2=32+42=25,
∴①当OP2+PD2=OD2时,
即9+m2+m2+6m+10=25,
解得:m=$\frac{-3±\sqrt{21}}{2}$,
②当OP2+OD2=PD2时,
即9+m2+25=m2+6m+10,
解得:m=4,
③当OP2=OD2+PD2时,
即9+m2=m2+6m+10+25,
解得:m=-$\frac{13}{3}$,
∴点P的坐标为:(3,$\frac{-3+\sqrt{21}}{2}$),(3,$\frac{-3-\sqrt{21}}{2}$),(3,4),(3,-$\frac{13}{3}$).
点评 本题考查了二次函数综合题,利用了自变量与函数值的对应关系是求点与坐标轴的交点坐标的关键,待定系数求函数解析式,相似三角形的判定:两角对应相等的两个三角形相似,两边对应成比例且夹角相等的两个三角形相似;勾股定理的应用.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案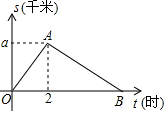 某单位在小绿谷举办“民族团结一家亲”徒步活动,某人从起点出发,以4千米/小时的平均速度走了2小时到达终点,之后再沿原路返回,设此人离开起点的路程s(千米)与步行时间t(小时)之间的函数关系如图所示.根据图象提供信息,解答下列问题:
某单位在小绿谷举办“民族团结一家亲”徒步活动,某人从起点出发,以4千米/小时的平均速度走了2小时到达终点,之后再沿原路返回,设此人离开起点的路程s(千米)与步行时间t(小时)之间的函数关系如图所示.根据图象提供信息,解答下列问题: