题目内容
7.已知函数y1=-$\frac{1}{3}$x2,y2=-$\frac{1}{3}$x2+3和y3=-$\frac{1}{3}$x2-1,y4=-$\frac{1}{3}$x2+6.(1)分别画出它们的图象;
(2)说出各个图象的开口方向、对称轴和顶点坐标;
(3)试说明函数y2=-$\frac{1}{3}$x2+3,y3=-$\frac{1}{3}$x2-1,y4=-$\frac{1}{3}$x2+6的图象分别由抛物线y1=-$\frac{1}{3}$x2作怎样的平移才能得到?
分析 (1)将四个抛物线的图象画出来即可;
(2)结合函数图象及解析式,即可得出抛物线的开口方向、对称轴和顶点坐标;
(3)根据平移的性质,叙述出其它三个函数图象是如何由抛物线y1=-$\frac{1}{3}$x2作怎样的平移得到的即可.
解答 解:(1)依照题意,画出图形,如图所示.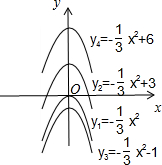
(2)根据函数图象,可知:
4个函数图形开口均向下,对称轴均为直线x=0,函数y1=-$\frac{1}{3}$x2的顶点为(0,0);函数y2=-$\frac{1}{3}$x2+3的顶点为(0,3);函数y3=-$\frac{1}{3}$x2-1的顶点为(0,-1);函数y4=-$\frac{1}{3}$x2+6的顶点为(0,6).
(3)函数y2=-$\frac{1}{3}$x2+3的图象是由抛物线y1=-$\frac{1}{3}$x2的图象向上平移3个单位长度得来的;函数y3=-$\frac{1}{3}$x2-1的图象是由抛物线y1=-$\frac{1}{3}$x2的图象向下平移1个单位长度得来的;函数y4=-$\frac{1}{3}$x2+6的图象是由抛物线y1=-$\frac{1}{3}$x2的图象向上平移6个单位长度得来的.
点评 本题考查了二次函数图象与几何变换,解题的关键是熟练掌握二次函数的图象及二次函数的性质.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
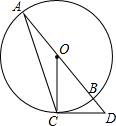 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接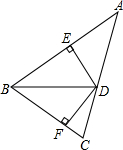 如图:BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=18cm2,
如图:BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=18cm2,