题目内容
5. 如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为7和11,则△CDE的面积为$\sqrt{7}$.
如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为7和11,则△CDE的面积为$\sqrt{7}$.
分析 过E点和G点分别作△CDE和△DGF的高CP和GH,证明△DCP与△DGH全等,得出CP=DH,再根据勾股定理求出DH=AG,通过求三角形的面积可得到答案.
解答 解:过E点和G点分别作△CDE和△DGF的高CP和GH,
∵DGFC是正方形,
∴DG=DE,∠EDG=90°,
∵∠EDP+∠HDG=90°
∵∠EDP+∠DEP=90°,
∴∠HDG=∠DEP,
在△EDP与△DGH中,
$\left\{\begin{array}{l}{∠EPD=∠DHG=90°}\\{∠EDP=∠DGH}\\{DE=DG}\end{array}\right.$
∴△EDP≌△DGH(AAS),
∴DH=PE,
∵∠DAG=∠DHG=90°,∠ADH=∠AGH=90°
∴四边形ADHG是矩形,
∴AG=DH,
∵正方形ABCD和正方形DEFG的面积分别为7和11,
∴CD=AD=$\sqrt{7}$,DG=$\sqrt{11}$,
在Rt△ADG中,
$AG=\sqrt{D{G}^{2}-A{D}^{2}}=\sqrt{11-7}=2$,
∴PE=2,
∴△CDE的面积=$\frac{1}{2}CD•PE=\frac{1}{2}×\sqrt{7}×2=\sqrt{7}$,
故答案为:$\sqrt{7}$.
点评 此题考查全等三角形的判定和性质,关键是构建全等三角形,同时应用勾股定理求边长.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
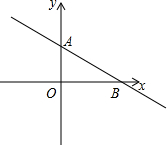 如图,直线AB与y轴,x轴交点分别为A(0,2),B(4,0),
如图,直线AB与y轴,x轴交点分别为A(0,2),B(4,0),