题目内容
17.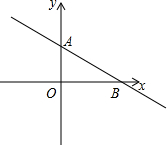 如图,直线AB与y轴,x轴交点分别为A(0,2),B(4,0),
如图,直线AB与y轴,x轴交点分别为A(0,2),B(4,0),问题1:求直线AB的解析式及△AOB的面积;
问题2:观察函数图象,直接回答:当x满足什么条件时,①y>0,②y=0,③y<0.
分析 问题1:设直线AB的解析式为y=kx+b(k≠0),将点A、B的坐标代入函数解析式列出关于k和b的方程组,通过解方程组求得它们的值;然后根据三角形的面积公式来求△AOB的面积;
问题2:①当直线在x轴上方时,y>0;②直线与x轴相交时,y=0;③直线在x轴下方时,y<0.
解答 解:问题1:设直线AB的解析式为y=kx+b(k≠0),则
$\left\{\begin{array}{l}{b=2}\\{4k+b=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
则该直线的解析式为:y=-$\frac{1}{2}$x+2.
∵A(0,2)、B(4,0),
∴OA=2,OB=4,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×2×4=4,即△AOB的面积是4;
问题2:观察函数图象,可得①当x<4时,y>0,②当x=4时,y=0,③当x>4时,y<0.
点评 本题考查了待定系数法求一次函数解析式,三角形的面积,利用数形结合根据函数图象求不等式的解集、方程的解是常用的方法,要熟练掌握并灵活运用.

练习册系列答案
相关题目
8.计算(-3)2n+1+3•(-3)2n的结果是( )
| A. | 34n+2 | B. | 2•32n+1 | C. | -2•32n+1 | D. | 0 |
12.甲、乙两班学生到集市购买水果,苹果价格如下:
甲班分两次共购买苹果70千克(第二次多于第一次),共付189元;乙班一次购买苹果70千克.
(1)乙班买苹果付了140元;
(2)乙班比甲班少付了49元;
(3)甲班第一次、第二次分别购买苹果多少千克?
| 购买苹果数量 | 不超过30千克 | 超30千克但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
(1)乙班买苹果付了140元;
(2)乙班比甲班少付了49元;
(3)甲班第一次、第二次分别购买苹果多少千克?
9.计算:a•$\sqrt{2a}$•5$\sqrt{6ab}$的结果是( )
| A. | 10a2$\sqrt{3b}$ | B. | 60a3b | C. | 5a2$\sqrt{12b}$ | D. | 5a$\sqrt{12b}$ |
7. 如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )
如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )
 如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )
如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )| A. | 祝 | B. | 考 | C. | 试 | D. | 顺 |
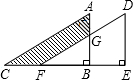 如图,将直角△ABC沿CB方向平移BE的距离得到直角△DEF,已知AG=2,BE=4,DE=6,求图中阴影部分的面积.
如图,将直角△ABC沿CB方向平移BE的距离得到直角△DEF,已知AG=2,BE=4,DE=6,求图中阴影部分的面积. 如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为7和11,则△CDE的面积为$\sqrt{7}$.
如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为7和11,则△CDE的面积为$\sqrt{7}$.