题目内容
8.已知实数a,b,c满足:a2+b2+c2=ab+bc+ca,且2a+3b-4c=2,则a+b+c=6.分析 通过已知条件,需要求出a、b、c的值,把a2+b2+c2=ab+bc+ca两边都乘以2,然后根据完全平方公式整理得到a=b=c,再代入2a+3b-4c=2求出a的值,然后代入代数式计算即可.
解答 解:∵a2+b2+c2=ab+bc+ca,
∴2(a2+b2+c2)=2(ab+bc+ca),
即2(a2+b2+c2)-2(ab+bc+ca)=0,
整理,得(a2-2ab+b2)+(a2-2ca+c2)+(b2-2bc+c2)=0,
即:(a-b)2+(a-c)2+(b-c)2=0,
∴a=b=c,
又∵2a+3b-4c=2,
∴a=b=c=2.
∴a+b+c=2+2+2=6.
故答案为:6.
点评 本题考查了因式分解的应用,巧妙地用到了完全平方公式,把已知条件转化为一个完全平方式,再由平方数非负数的性质,得出三个未知数间的相等关系,从而求得三个未知数的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,∠B=38°,∠C=40°,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则∠DAE=24°.
如图,在△ABC中,∠B=38°,∠C=40°,AB的垂直平分线交BC于D,AC的垂直平分线交BC于E,则∠DAE=24°.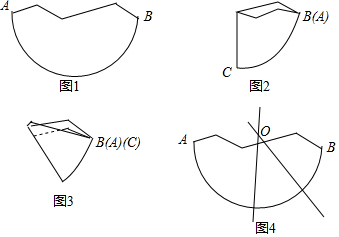 数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:
数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下: