题目内容
16. 数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:
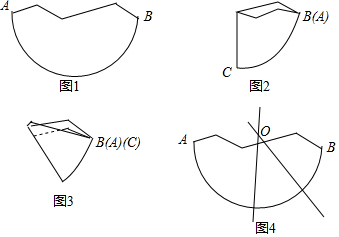
数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:第一步:如图1,将残缺的纸片对折,使$\widehat{AB}$的端点A与端点B重合,得到图2;
第二步:将图2继续对折,使$\widehat{CB}$的端点C与端点B重合,得到图3;
第三步:将对折后的图3打开如图4,两条折痕所在直线的交点即为圆心O.
老师肯定了他的作法.那么他确定圆心的依据是轴对称图形的性质及圆心到圆上各点的距离相等.
分析 由圆心到圆上各点的距离相等知圆心在AB和BC的中垂线上,再结合轴对称图形的性质知两条折痕即为AB、BC的中垂线,从而得出答案.
解答 解:如图,
第一步对折由轴对称图形可知OC是AB的中垂线,点O在AB中垂线上;
第二步对折由轴对称图形可知OD是BC的中垂线,点O在BC中垂线上;
从而得出点O在AB、BC中垂线交点上,
故答案为:轴对称图形的性质及圆心到圆上各点的距离相等.
点评 本题主要考查圆的基本性质和轴对称图形的性质,熟练掌握圆心到圆上各点的距离相等及中垂线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6.倒数大于它本身的是( )
| A. | 1 | B. | 假分数 | C. | 真分数 | D. | 无法判断 |
11.某农场引进一批新稻种,在播种前做了五次发芽实验,每次任取800粒稻种进行实验.实验的结果如下表所示:
在与实验条件相同的情况下,估计种一粒这样的稻种发芽的概率为0.95(精确到0.01);如果该农场播种了此稻种2万粒,那么能发芽的大约有1.9万粒.
| 实验的稻种数n∕粒 | 800 | 800 | 800 | 800 | 800 |
| 发芽的稻种数m∕粒 | 763 | 757 | 761 | 760 | 758 |
| 发芽的频率$\frac{m}{n}$ | 0.954 | 0.946 | 0.951 | 0.950 | 0.948 |
6. 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | 2π-2$\sqrt{3}$ | C. | $\frac{2}{3}$π-$\sqrt{3}$ | D. | $\frac{1}{3}$π |
 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF=15°.
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF=15°. 如图,已知斜坡 AB 的坡度为 1:3.若坡长 AB=10m,则坡高 BC=$\sqrt{10}$m.
如图,已知斜坡 AB 的坡度为 1:3.若坡长 AB=10m,则坡高 BC=$\sqrt{10}$m.