题目内容
19．
如图，在△ABC中，∠A=90°，⊙A切BC于点D，BD=4，CD=9，求⊙A的半径．
分析 连接AD，构造相似三角形：△ABD∽△CAD．再通过比例线段可求出AD．AD就是半径．
解答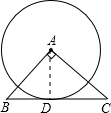 
解：如图，连接AD．
∵⊙A切BC于D，
∴AD⊥BC．
又∵∠BAD+∠ABD=90°，∠BAD+∠CAD=90°，
∴△ABD∽△CAD．
∴$\frac{AD}{BD}$=$\frac{CD}{AD}$，
∴AD2=BD•CD．
∴AD=$\sqrt{4×9}$=6．
∴⊙A的半径是6．
点评 此题考查了切线的性质定理，相似三角形的判定和性质，正确的作出辅助线三角解题的关键．
练习册系列答案
相关题目
14．某饮料加工厂从所生产的瓶装饮料中抽取了50瓶检查质量，质量超过标准质量的用正数表示，质量低于标准质量的用负数表示，结果记录如表：
（1）这50瓶饮料平均每瓶的质量比每瓶的标准质量多多少克？
（2）若这种饮料每瓶的标准质量是400克，求这50瓶饮料的总质量．
| 与标准质量的偏差（单位：克） | -7 | -6 | -1 | 0 | 5 | 10 |
| 瓶数 | 4 | 6 | 10 | 13 | 9 | 8 |
（2）若这种饮料每瓶的标准质量是400克，求这50瓶饮料的总质量．
11．
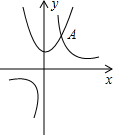如图，抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2，则关于x的不等式$\frac{k}{x}$+x2+2＜0的解是（ ）
如图，抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2，则关于x的不等式$\frac{k}{x}$+x2+2＜0的解是（ ）| A． | 0＜x＜2 | B． | -2＜x＜0 | C． | x＞2 | D． | x＜-2 |