题目内容
6. 如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若△ABC的面积为20cm2,则四边形A1DCC1的面积为( )
如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若△ABC的面积为20cm2,则四边形A1DCC1的面积为( )| A. | 10 cm2 | B. | 12 cm2 | C. | 15 cm2 | D. | 17 cm2 |
分析 根据题意可知:CD∥A1C1,则△B1DC∽△B1A1C1,根据相似三角形面积比等于相似比的平方求出△B1DC的面积,则四边形A1DCC1的面积=△ABC的面积-△B1DC的面积.
解答 解:由题意得:B1是BC的中点,C是B1C1的中点,
∵CD∥A1C1,
∴△B1DC∽△B1A1C1,
∴$\frac{{S}_{△{B}_{1}DC}}{{S}_{△{B}_{1}{C}_{1}{A}_{1}}}$=$\frac{1}{4}$,
∵S△ABC=${S}_{△{B}_{1}{A}_{1}{C}_{1}}$=20,
∴${S}_{△{B}_{1}DC}$=5,
∴四边形A1DCC1的面积=20-5=15,
故选C.
点评 本题考查了平移变换和相似三角形的性质,要知道平移前后图形的对应线段相等且平行或在同一直线上,求图形面积时,可以直接求或间接利用和或差求,本题求的是不规则四边形的面积,所以间接利用差来求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列各组数中的互为相反数的是( )
| A. | 3与$\frac{1}{3}$ | B. | (-1)2与1 | C. | -24与 24 | D. | -(-2)与|-2| |
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\sqrt{20}$ | D. | $\sqrt{x+3}$ |
 如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=$\frac{{k}_{1}}{x}$的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点D(n,-2).
如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=$\frac{{k}_{1}}{x}$的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点D(n,-2).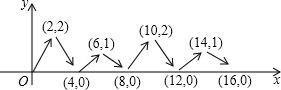 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第36次运动后,动点P的坐标是(72,0).
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第36次运动后,动点P的坐标是(72,0).
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象,根据图形判断①abc>0;②a+b+c<0;③2a+b>0;④b2-4ac>4a中正确的个数有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象,根据图形判断①abc>0;②a+b+c<0;③2a+b>0;④b2-4ac>4a中正确的个数有( ) 如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.
如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.