题目内容
5. 如图,已知P为等边△ABC内的一点,且PA=5,PB=3,PC=4,将线段BP绕点P按逆时针方向旋转60°至PQ的位置.
如图,已知P为等边△ABC内的一点,且PA=5,PB=3,PC=4,将线段BP绕点P按逆时针方向旋转60°至PQ的位置.(1)求证:△ABP≌△CBQ
(2)求证:∠BPC=150°.
分析 (1)根据SAS即可证明.
(2))由△ABP≌△CBQ,推出PA=QC=4,由BP=BQ,∠PBQ=60°,推出△PBQ是等边三角形,由PQ=3,∠BPQ=60°,在△PQC中,PC2+PQ2=43+32=52=QC2,推出△PQC是直角三角形,推出∠QPC=90°,即可得出∠BPC=∠BPQ+∠QPC=150°.
解答 证明:(1)∵BP=BQ,∠PBQ=60°,
又∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∴∠PBQ=∠ABC,
∴∠ABP=∠CBQ,
在△ABP和△CBQ中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABP=∠CBQ}\\{BP=BQ}\end{array}\right.$,
∴△ABP≌△CBQ.
(2)∵△ABP≌△CBQ,
∴PA=QC=4,
∵BP=BQ,∠PBQ=60°,
∴△PBQ是等边三角形,
∴PQ=3,∠BPQ=60°,
∵在△PQC中,PC2+PQ2=43+32=52=QC2,
∴△PQC是直角三角形,
∴∠QPC=90°,
∴∠BPC=∠BPQ+∠QPC=60°+90°=150°.
点评 本题考查了旋转的性质,等边三角形的判定与性质,勾股定理逆定理,熟记性质与等边三角形的判断方法是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
13.计算:
(1)$\frac{500}{(a-1)^{2}}$÷$\frac{500}{{a}^{2}-1}$;
(2)(m+2+$\frac{5}{2-m}$)•$\frac{2-m}{3-m}$.
(1)$\frac{500}{(a-1)^{2}}$÷$\frac{500}{{a}^{2}-1}$;
(2)(m+2+$\frac{5}{2-m}$)•$\frac{2-m}{3-m}$.
10.观察如下所示规律排列的数组,{1},{2,3},{4,5,6},…,(从第二组开始,每组中数的个数都比前一组多一个),若假定某个数所在的组数为a,并且是这个组内的第b个数,那么2017这个数所对应的a、b分别为( )
| A. | 64,1 | B. | 63,62 | C. | 63,1 | D. | 63,63 |
17.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{12}$-$\sqrt{10}$=$\sqrt{2}$ | D. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ |
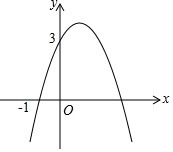 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).