题目内容
3. 如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,则重叠部分(△BEF)的面积为7.5cm2.
如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,则重叠部分(△BEF)的面积为7.5cm2.
分析 设DE=xcm,由翻折的性质可知DE=EB=x,则AE=(9-x)cm,在Rt△ABE中,由勾股定理求得ED的长;由翻折的性质可知∠DEF=∠BEF,由矩形的性质可知BC∥AD,从而得到∠BFE=∠DEF,故此可知∠BFE=∠FEB,得出FB=BE,最后根据三角形的面积公式求解即可.
解答 解:设DE=xcm.
由翻折的性质可知DE=EB=x,∠DEF=∠BEF,则AE=(9-x)cm.
在Rt△ABE中,由勾股定理得;BE2=EA2+AB2,即x2=(9-x)2+32.
解得:x=5.
∴DE=5cm.
∵四边形ABCD为矩形,
∴BC∥AD.
∴∠BFE=∠DEF.
∴∠BFE=∠FEB.
∴FB=BE=5cm.
∴△BEF的面积=$\frac{1}{2}$BF•AB=$\frac{1}{2}$×3×5=7.5(cm2);
故答案为:7.5cm2.
点评 本题主要考查的是翻折的性质、勾股定理的应用,等腰三角形的判定、三角形的面积公式,证得△BEF为等腰三角形,从而得到FB的长是解题的关键.

练习册系列答案
相关题目
12.地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,地球的体积约是太阳体积的倍数是( )
| A. | 7.1×10-6 | B. | 7.1×10-7 | C. | 1.4×106 | D. | 1.4×107 |
 某市2012~2016年春节期间烟花爆竹销售量统计如图所示,根据统计图中提供的信息,预估2017年该市春节期间烟花爆竹销售量约为8万箱,你的预估理由是2012到2015年销售量下降明显,但2015到2015年下降趋势变缓.
某市2012~2016年春节期间烟花爆竹销售量统计如图所示,根据统计图中提供的信息,预估2017年该市春节期间烟花爆竹销售量约为8万箱,你的预估理由是2012到2015年销售量下降明显,但2015到2015年下降趋势变缓.
 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为$\frac{7}{2}$.
如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为$\frac{7}{2}$.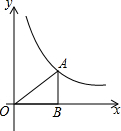 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为2$\sqrt{6}$+4.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为2$\sqrt{6}$+4.