Question

7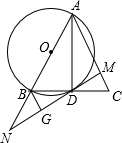．如图，已知在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过D作MN⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于G．
（1）判断△ABC的形状，并证明你的结论；
（2）求证：直线MN是⊙O的切线；
（3）求证：△BGD∽△DMA．

Answer 1

分析 （1）根据圆周角定理求得AD⊥BC，即可得出AD是BC的垂直平分线，根据垂直平分线的性质得出AB=AC，即可证得△ABC为等腰三角形．
（2）连结OD．由三角形中位线的性质得出OD∥AC，MN⊥AC，可得OD⊥MN，然后根据切线的判定定理即可证明直线MN是⊙O的切线；
（3）根据垂直定义得出∠BGD=∠DMA=90°，由圆周角定理、三角形内角和定理、对顶角性质及等角的余角相等得出∠DBG=∠ADM，再根据两角对应相等的两三角形相似即可证明△BGD∽△DMA．

解答 证明：（1）△ABC为等腰三角形．
∵AD是BC边上的中线
∴BD=CD
∵以AB为直径的⊙O交BC于点D，
∴AD⊥BC，
∴AD是BC的垂直平分线，
∴AB=AC，
∴△ABC为等腰三角形．
（2）连结OD．
∵BO=OA，BD=DC，
∴OD是△ABC的中位线，
∴OD∥AC．
∵MN⊥AC，
∴OD⊥MN，
∴直线MN是⊙O的切线．     
（3）∵MN⊥AC于点M，BG⊥MN于G，
∴∠BGD=∠DMA=90°．
∵以AB为直径的⊙O交BC于点D，∴AD⊥BC，∠ADB=90°，
∴∠ADM+∠BDG=90°，
∵∠DBG+∠BDG=90°，
∴∠DBG=∠ADM．
∴△BGD∽△DMA．

点评 本题主要考查了切线的判定，相似三角形的判定．要证某线是圆的切线，已知此线过圆上某点，连结圆心与这点（即为半径），再证垂直即可．