题目内容
18.已知菱形ABCD的边长为5,两条对角线AC,BD相交于O点,且AO,BO的长(AO<BO)分别是一元二次方程x2-(2m-1)x+4(m-1)=0的根,求m的值及AC、BD的长.分析 根据菱形的性质得出AB=AD=CD=BC=5,AC⊥BD,AC=2AO,BD=2BO,求出∠AOB=90°,根据勾股定理得出AO2+BO2=25,根据根与系数的关系得出AO+BO=2m-1,AO×BO=4(m-1),变形后代入求出m的值,即可得出答案.
解答 解:
∵四边形ABCD是菱形,
∴AB=AD=CD=BC=5,AC⊥BD,AC=2AO,BD=2BO,
∴∠AOB=90°,
∴AO2+BO2=AB2=52=25,
∵AO,BO的长(AO<BO)分别是一元二次方程x2-(2m-1)x+4(m-1)=0的根,
∴AO+BO=2m-1,AO×BO=4(m-1),
∴AO2+BO2=(AO+BO)2-2AO×BO=25,
∴(2m-1)2-8(m-1)=25,
解得:m1=4,m2=-1,
∵AO+BO=2m-1,AO×BO=4(m-1),
∴当m=-1时,AO×BO=-8<0,不符合题意,舍去,
即m=4,
则AO+BO=7且AO×BO=12,
∵AO<BO,
∴AO=3,BO=4,
∴AC=2AO=6,BD=2BO=8.
点评 本题考查了菱形的性质,勾股定理,根与系数的关系的应用,能得出关于m的方程是解此题的关键,注意:菱形的对角线互相平分且相等.

练习册系列答案
相关题目
13.下列几种说法中,不正确的( )
| A. | 任意有理数a的相反数是-a | |
| B. | 在一个数前面加上“-”号所得的数是负数 | |
| C. | 一个非0有理数a的倒数是$\frac{1}{a}$ | |
| D. | 最小的自然数是0 |
3.下列是二次函数的是( )
| A. | y=2(x+1)2 | B. | y=4x2-(2x+1)2 | C. | y=$\frac{{x}^{2}}{x}$ | D. | y=$\frac{1}{{x}^{2}}$ |
7. 如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
 如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )| A. | 2$\sqrt{3}$cm | B. | 3cm | C. | 4cm | D. | 2$\sqrt{5}$cm |
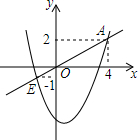 如图,二次函数y=x2+bx+c的图象与正比例函数y=kx的图象相交于点A(4,2)和点B(m,-1),求该二次函数与正比例函数的解析式.
如图,二次函数y=x2+bx+c的图象与正比例函数y=kx的图象相交于点A(4,2)和点B(m,-1),求该二次函数与正比例函数的解析式.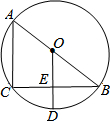 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.