题目内容
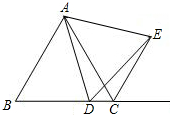 如图,已知△ABC为等边三角形,∠ADE=60°,CE为外角角平分线,求证:△ADE为等边三角形.
如图,已知△ABC为等边三角形,∠ADE=60°,CE为外角角平分线,求证:△ADE为等边三角形.考点:等边三角形的判定与性质
专题:证明题
分析:过D作DG∥AC交AB于G,得出∠ADG=∠DEC,再利用AAS得出△AGD≌△DCE,进而得出答案
解答: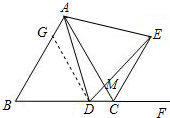 证明:过D作DG∥AC交AB于G,
证明:过D作DG∥AC交AB于G,
则∠DAC=∠ADG,∠BGD=∠BAC=60°,
∴∠AGD=120°,
∵∠B=60°,
∴△GDB为等边三角形,
∴BG=BD,
∵△ABC是等边三角形,
∴∠ACF=120°,AB=BC,
∴AG=DC,
∵CE平分∠ACE,
∴∠ACE=∠ECF=60°,
∴∠DCE=120°,
∴∠AGD=∠DCE,
∵∠AMD=∠EMC,
∵∠ADE=60°=∠ACE,
∴∠DAC=∠DEC=∠ADG,
在△AGD和△DCE中,
,
∴△AGD≌△DCE(AAS),
∴AD=DE,
∵∠ADE=60°,
∴△ADE是等边三角形.
 证明:过D作DG∥AC交AB于G,
证明:过D作DG∥AC交AB于G,则∠DAC=∠ADG,∠BGD=∠BAC=60°,
∴∠AGD=120°,
∵∠B=60°,
∴△GDB为等边三角形,
∴BG=BD,
∵△ABC是等边三角形,
∴∠ACF=120°,AB=BC,
∴AG=DC,
∵CE平分∠ACE,
∴∠ACE=∠ECF=60°,
∴∠DCE=120°,
∴∠AGD=∠DCE,
∵∠AMD=∠EMC,
∵∠ADE=60°=∠ACE,
∴∠DAC=∠DEC=∠ADG,
在△AGD和△DCE中,
|
∴△AGD≌△DCE(AAS),
∴AD=DE,
∵∠ADE=60°,
∴△ADE是等边三角形.
点评:本题主要考查了全等三角形的判定与性质以及等边三角形的性质等知识,正确得出辅助线是解题关键.

练习册系列答案
相关题目
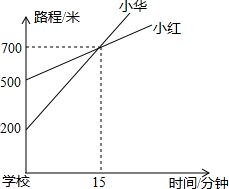 如图,小红和小华分别从A、B两地到远离学校的博物馆(A地、B地、学校、博物馆在一条直线上),小红步行,小华骑车.
如图,小红和小华分别从A、B两地到远离学校的博物馆(A地、B地、学校、博物馆在一条直线上),小红步行,小华骑车.  如图,已知梯形上下底边的长分别为36和60,高为32,这个梯形两腰的延长线的交点到两底的距离分别是多少?
如图,已知梯形上下底边的长分别为36和60,高为32,这个梯形两腰的延长线的交点到两底的距离分别是多少? 已知:如图,点E、F在AC上,AB∥CD,AB=CD,AE=CF.求证:△ABE≌△CDF.
已知:如图,点E、F在AC上,AB∥CD,AB=CD,AE=CF.求证:△ABE≌△CDF.