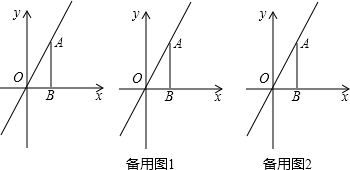
题目内容
12.一根蜡烛高20cm,蜡烛高度 y(单位:cm)随燃烧的时间x(单位:分钟)的增加而减少,平均每分钟减少量为0.1cm/分钟.求y与x的函数关系式,并画出该函数的图象.分析 根据蜡烛的高度=20-每分钟燃烧的长度×时间,建立函数关系式用待定系数法求解;令y=0即可求得燃烧完使用的时间;根据自变量的取值范围知:此图象是一条线段,而不能画成直线或射线.
解答 解:根据题意得:y=20-0.1x,
当y=0时,20-0.1x=0,
x=200,
即点燃200分钟后可燃烧光;
由x的取值范围:0≤x≤200,图象是一条线段.
如图所示:
点评 本题考查了一次函数的应用,解决本题的关键是能够根据题意中的等量关系建立函数关系式;能够根据函数解析式求得对应的x的值;画图象的时候,特别注意自变量的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.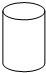 如图是一个圆柱体,则它的主视图是( )
如图是一个圆柱体,则它的主视图是( )
 如图是一个圆柱体,则它的主视图是( )
如图是一个圆柱体,则它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
20.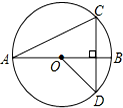 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
7.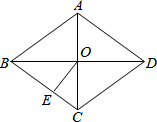 如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
 如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )| A. | S=AC•BD | B. | S=4BC•OE | C. | S=2AB•OE | D. | S=2BD•AO |
1.从A地向B地打长途电话,通话时间不超过3min收费2.4元,超过3min后每分加收1元.
(Ⅰ)根据题意,填写下表:
(Ⅱ)设通话时间为xmin,通话费用y元,求y与x的函数解析式;
(Ⅲ)若小红有10元钱,求她打一次电话最多可以通话的时间(本题中通话时间取整数,不足1min的通话时间按1min计费).
(Ⅰ)根据题意,填写下表:
| 通话时间min | 2 | 3 | 6 | … |
| 通话费用/元 | 2.4 | 2.4 | 5.4 | … |
(Ⅲ)若小红有10元钱,求她打一次电话最多可以通话的时间(本题中通话时间取整数,不足1min的通话时间按1min计费).