题目内容
 ①如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.
①如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论;
②如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC,交CE的延长线与点F.求证:AB垂直平分DF.
分析:①(1)由三角形中位线知识可得EF=GH,EF∥GH,∴四边形EFGH是平行四边形.
(2)要是菱形,只需增加相邻两边相等,如要得到EF=GF,由中位线知识,只须AB=CD.
②∵FB∥AC,∠ACB=90°∴∠FBC=90°,由AC=BC、∠ACB=90°∴∠DBA=45°,AB是∠CBF平分线.证明Rt△ADC≌Rt△FBC,所以DB=FB,所以,AB垂直平分DF(等腰三角形中的三线合一定理).
(2)要是菱形,只需增加相邻两边相等,如要得到EF=GF,由中位线知识,只须AB=CD.
②∵FB∥AC,∠ACB=90°∴∠FBC=90°,由AC=BC、∠ACB=90°∴∠DBA=45°,AB是∠CBF平分线.证明Rt△ADC≌Rt△FBC,所以DB=FB,所以,AB垂直平分DF(等腰三角形中的三线合一定理).
解答:①(1)证明:
∵E、F分别是AD、BD中点,
∴EF∥AB,EF=
AB,
同理GH∥AB,GH=
AB,
∴EF=GH,EF∥GH,∴四边形EFGH是平行四边形.
(2)解:当四边形ABCD满足AB=CD时,四边形EFGH是菱形.
证明:F、G分别是BD、BC中点,所以GF=
CD,
∵AB=CD,∴EF=GF
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
②证明:∵∠ACB=90°,Rt△ADC中,∠1+∠2=90°,
∵AD⊥CF,在Rt△EDC中,∠3+∠2=90°,得:∠1=∠3.
∵FB∥AC,∠ACB=90°,∴∠FBC=90°,得:△FBC是直角三角形.
∵AC=BC,∠1=∠3,△FBC是直角三角形
∴Rt△ADC≌Rt△FBC.
∴CD=FB,已知CD=DB,可得:DB=FB.
由AC=BC、∠ACB=90°,可得:∠4=45°,AB是∠CBF平分线.
所以,AB垂直平分DF(等腰三角形中的三线合一定理).
∵E、F分别是AD、BD中点,
∴EF∥AB,EF=
| 1 |
| 2 |
同理GH∥AB,GH=
| 1 |
| 2 |
∴EF=GH,EF∥GH,∴四边形EFGH是平行四边形.
(2)解:当四边形ABCD满足AB=CD时,四边形EFGH是菱形.
证明:F、G分别是BD、BC中点,所以GF=
| 1 |
| 2 |
∵AB=CD,∴EF=GF
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形.
②证明:∵∠ACB=90°,Rt△ADC中,∠1+∠2=90°,

∵AD⊥CF,在Rt△EDC中,∠3+∠2=90°,得:∠1=∠3.
∵FB∥AC,∠ACB=90°,∴∠FBC=90°,得:△FBC是直角三角形.
∵AC=BC,∠1=∠3,△FBC是直角三角形
∴Rt△ADC≌Rt△FBC.
∴CD=FB,已知CD=DB,可得:DB=FB.
由AC=BC、∠ACB=90°,可得:∠4=45°,AB是∠CBF平分线.
所以,AB垂直平分DF(等腰三角形中的三线合一定理).
点评:本题考查了中位线知识,平行四边形和菱形的判断方法.

练习册系列答案
相关题目
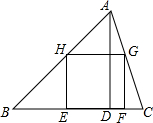 如图,四边形EFGH是△ABC内接正方形,BC=21cm,高AD=15cm,则内接正方形EFGH的边长是多少?
如图,四边形EFGH是△ABC内接正方形,BC=21cm,高AD=15cm,则内接正方形EFGH的边长是多少? 如图,在△ABC中,若DE是△ABC的中位线,△ABC的面积是8.求四边形DBCE的面积.
如图,在△ABC中,若DE是△ABC的中位线,△ABC的面积是8.求四边形DBCE的面积.
 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm.求四边形DEFG的周长.
如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm.求四边形DEFG的周长. 如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.
如图,在△ABC中,点D是边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.