题目内容
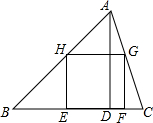如图，四边形EFGH是△ABC内接正方形，BC=21cm，高AD=15cm，则内接正方形EFGH的边长是多少？
分析：根据题意易证△AHG∽△ABC，列出比例关系，可以解出内接正方形EFGH的边长．
解答：
解：设AD与HG的交点为M，
由题意知，
∵四边形EFGH是△ABC内接正方形，
∴HG∥BC，
∴△AHG∽△ABC，
∴
=
，
=
，
解得HG=
，
故内接正方形EFGH的边长为
．
解：设AD与HG的交点为M，由题意知，
∵四边形EFGH是△ABC内接正方形，
∴HG∥BC，
∴△AHG∽△ABC，
∴
| HG |
| BC |
| AM |
| AD |
| HG |
| 21 |
| 15-HG |
| 15 |
解得HG=
| 35 |
| 4 |
故内接正方形EFGH的边长为
| 35 |
| 4 |
点评：本题主要考查正方形的性质，三角形相似等知识点，不是很难．
练习册系列答案
相关题目
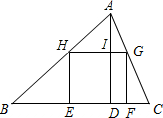如图，四边形EFGH是△ABC内接正方形，BC=27cm，高AD=21cm，求内接正方形EFGH的面积．
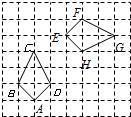8、如图，四边形EFGH是由四边形ABCD经过旋转得到的．如果用有序数对（2，1）表示方格纸上A点的位置，用（1，2）表示B点的位置，那么四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是
4、如图，四边形EFGH是由四边形ABCD平移得到的，已知AD=5，∠B=70°，则（ ）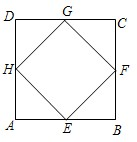
四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
如图，四边形EFGH是△ABC内接正方形，BC=21cm，高AD=15cm．