题目内容
7.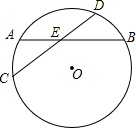 如图,⊙0的弦CD平分AB,交点为E.
如图,⊙0的弦CD平分AB,交点为E.(1)求证:BE是CE、DE的比例中项;
(2)若AB=12cm,CD=13cm,求CE和DE的长.
分析 (1)连接AC,BD,根据圆周角定理得到∠C=∠B.∠A=∠D,推出△AEC∽△BDE,即可得到结论;
(2)由(1)证得BE2=CE•DE,求得CE•DE=36cm,即CE(CD-CE)=CE(13-CE)=36,解方程即可得到结论.
解答 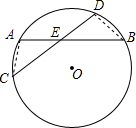 (1)证明:连接AC,BD,
(1)证明:连接AC,BD,
∵∠C=∠B.∠A=∠D,
∴△AEC∽△BDE,
∴$\frac{AE}{CE}=\frac{DE}{BE}$,
∴AE•BE=CE•DE,
∵CD平分AB,
∴AE=BE,
∴BE2=CE•DE,
即BE是CE、DE的比例中项;
(2)解:∵AB=12cm,CD=13cm,
∴AE=BE=6cm,CE+DE=13cm,
由(1)证得BE2=CE•DE,
∴CE•DE=36cm,
即CE(CD-CE)=CE(13-CE)=36,
解得:CE=4,或CE=9,
∴DE=9,或DE=4.
点评 本题考查了相似三角形的判定和性质,圆周角定理,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19. 如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
 如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )| A. | a<b | B. | -a>b | C. | |a|<|b| | D. | -a>-b |
 如图,这是一个由小立方块搭成的几何体,请你分别画出从正面、左面、上面看到的形状.
如图,这是一个由小立方块搭成的几何体,请你分别画出从正面、左面、上面看到的形状. 如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.
如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.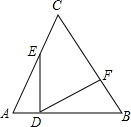 如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.
如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.