题目内容
11.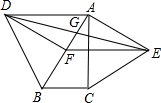 如图,分别以Rt△ABC的斜边AB,直角边AC为边向形外作等边△ABD和等边△ACE,F为AB 的中点.DE与AB相交于G,若∠BAC=30°,下列结论?:EF⊥AC;?AD=AE;?AD=4AG;?△DBF≌△EFA中,正确的有( )个.
如图,分别以Rt△ABC的斜边AB,直角边AC为边向形外作等边△ABD和等边△ACE,F为AB 的中点.DE与AB相交于G,若∠BAC=30°,下列结论?:EF⊥AC;?AD=AE;?AD=4AG;?△DBF≌△EFA中,正确的有( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据已知先判断△ABC≌△EFA,则∠AEF=∠BAC,得出EF⊥AC,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形,根据平行四边形的性质得出AD=4AG,从而得到答案.
解答 解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF=$\frac{1}{2}$BC,
∵BC=$\frac{1}{2}$AB,AB=BD,
∴HF=$\frac{1}{2}$BD;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),故④正确;
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∴AD≠AE,;
故②说法不正确;
∴AG=$\frac{1}{2}$AF,
∴AG=$\frac{1}{4}$AB,
∵AD=AB,
则AD=4AG,故③说法正确,
正确的有3个,
故选:C.
点评 本题考查了菱形的判定和性质,以及全等三角形的判定和性质,解决本题的关键是需先根据已知条件先判断出一对全等三角形,然后按排除法来进行选择.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知用4个矿泉水空瓶可换1瓶矿泉水,现有15个矿泉水空瓶若不再添钱,最多可喝矿泉水( )瓶.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.如果点(a,1-a)在第四象限,那么a的取值范围是( )
| A. | 0<a<1 | B. | -1<a<0 | C. | a<0 | D. | a>1 |
19. 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )
 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )| A. | a-b | B. | a+b | C. | a-2b | D. | 2a-b |
16.下列函数关系式中,表示y是x的反比例函数的是( )
| A. | y=$\frac{1}{{x}^{2}}$ | B. | y=$\sqrt{2}$x | C. | y=$\frac{5}{x}$ | D. | y=$\frac{x}{3}$ |
20.若|x+1|+(y-2)2=0,则xy的值是( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
1.已知△ABC中,∠C=90°,BC=3,AB=4,那么下列说法正确的是( )
| A. | sinB=$\frac{3}{5}$ | B. | cosB=$\frac{3}{4}$ | C. | tanB=$\frac{4}{3}$ | D. | cotB=$\frac{3}{4}$ |
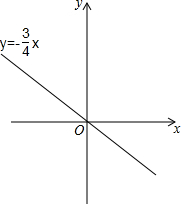 一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C.
一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C. 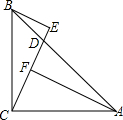 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,BE⊥CD,垂足为点E,AF⊥CD,垂足为点F,若$\frac{BD}{AD}$=$\frac{1}{2}$,AC=6$\sqrt{5}$,则DE=2.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,BE⊥CD,垂足为点E,AF⊥CD,垂足为点F,若$\frac{BD}{AD}$=$\frac{1}{2}$,AC=6$\sqrt{5}$,则DE=2.