题目内容
16.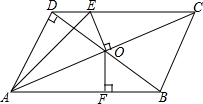 如图,在?ABCD中,BD是对角线,且BD⊥AD,OA=10cm,DB=12cm,OE⊥AC交CD于E,OF⊥AB于F
如图,在?ABCD中,BD是对角线,且BD⊥AD,OA=10cm,DB=12cm,OE⊥AC交CD于E,OF⊥AB于F(1)求△ADE的周长;
(2)求OF的长.
分析 (1)先证明AE=CE,再根据勾股定理求出AD、AB,即可得出结果;
(2)先证明△BFO∽△BDA,得出对应边成比例,即可求出OF.
解答 解:(1)∵四边形ABCD是平行四边形,
∴OA=OC=10,OD=$\frac{1}{2}$DB=6,AB=CD,
∵OE⊥AC,
∴AE=CE,
∵BD⊥AD,
∴∠BDA=90°,
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴CD=AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{8}^{2}+1{2}^{2}}$=4$\sqrt{13}$,
∴△ADE的周长=AD+DE+AE=AD+DE+CE=AD+CD=8+4$\sqrt{13}$;
(2)∵OF⊥AB,
∴∠BFO=90°,
∴∠BFO=∠BDA=90°,
又∵∠OBF=∠ABD,
∴△BFO∽△BDA,
∴$\frac{OF}{AD}=\frac{OB}{AB}$,即$\frac{OF}{8}=\frac{6}{4\sqrt{13}}$,
∴OF=$\frac{12\sqrt{13}}{13}$.
点评 本题考查了平行四边形的性质、线段垂直平分线的性质、勾股定理以及相似三角形的判定与性质;(1)把△ADE的周长转化为AD+CD以及(2)中证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
6.下列各式从左边到右边的变形是因式分解的是( )
| A. | x2+2x+1=x(x+2)+1 | B. | a2-6a+9=(a-3)2 | ||
| C. | (a+1)(a-1)=a2-1 | D. | -18x4y3=-6x2y2•3x2 |
5. 我省于2015年3月27日启动了2015年陕西省青少年校园足球活动,今年我省确定了265所校园足球特色学校,其中西安市有部分中小学入选,根据西安市各区中小学入选数据情况绘制了一幅不完整的统计表和一幅不完整的统计图.
我省于2015年3月27日启动了2015年陕西省青少年校园足球活动,今年我省确定了265所校园足球特色学校,其中西安市有部分中小学入选,根据西安市各区中小学入选数据情况绘制了一幅不完整的统计表和一幅不完整的统计图.
请根据图中提供的信息,回答下列问题:
(1)西安市总共有52所学校入选(精确到个位);
(2)未央区入选的学校占西安市入选学校的百分比为15%(百分号前边保留整数),雁塔区有12所学校入选(计算结果精确到个位)
(3)西安市各区入选学校的众数和中位数分别是多少?
 我省于2015年3月27日启动了2015年陕西省青少年校园足球活动,今年我省确定了265所校园足球特色学校,其中西安市有部分中小学入选,根据西安市各区中小学入选数据情况绘制了一幅不完整的统计表和一幅不完整的统计图.
我省于2015年3月27日启动了2015年陕西省青少年校园足球活动,今年我省确定了265所校园足球特色学校,其中西安市有部分中小学入选,根据西安市各区中小学入选数据情况绘制了一幅不完整的统计表和一幅不完整的统计图.| 城区名称 | 新城区 | 碑林区 | 莲湖区 | 灌桥区 | 未央区 | 雁塔区 | 汴东新城 |
| 入选学校数量 | 4所 | 9所 | 9所 | 6所 | 8所 | -- | 4所 |
(1)西安市总共有52所学校入选(精确到个位);
(2)未央区入选的学校占西安市入选学校的百分比为15%(百分号前边保留整数),雁塔区有12所学校入选(计算结果精确到个位)
(3)西安市各区入选学校的众数和中位数分别是多少?

 如图,梯形ABCD中,∠A=120°,BD平分∠ABC,且∠ABC=60°,求∠ADB的度数.
如图,梯形ABCD中,∠A=120°,BD平分∠ABC,且∠ABC=60°,求∠ADB的度数. 如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.
如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.