题目内容
7.在△ABC中,已知AB=6,AC=8,BC=10,则△ABC的外接圆半径是5.分析 根据勾股定理的逆定理知该三角形是直角三角形,则该三角形的外接圆的半径即为其斜边的一半.
解答 解:∵AC=8,BC=6,AB=10,
∴AC2+BC2=AB2,
∴∠C=90°.
则△ABC的外接圆半径长为$\frac{1}{2}$AB=5.
故答案为:5.
点评 此题考查了勾股定理的逆定理和直角三角形的外接圆的半径的求法,直角三角形外接圆的半径等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.一次函数y=-2015x+2015的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知关于a的一元二次方程5a2-a-11=0的两实数根分别为m,n,则直线y=-mnx+m+n一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.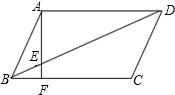 如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
 如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )| A. | 60° | B. | 66° | C. | 70° | D. | 72° |
19.方程x2-3x+4=0的根的情况是( )
| A. | 方程有两个不相等的实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程没有实数根 | D. | 无法确定 |
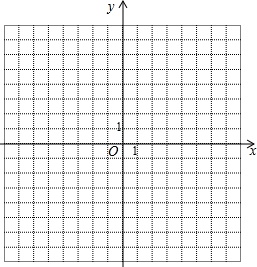 在如图所示的平面直角坐标系中完成下列任务:
在如图所示的平面直角坐标系中完成下列任务: