题目内容
16.△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c(1)若a:b=3:4,c=25,求a,b;
(2)若c-a=4,b=12,求a,c.
分析 (1)设a=3x,则b=4x,再根据勾股定理求出x的值,进而可得出结论.
(2)根据勾股定理可得a,b,c的数量关系,再把已知条件代入即可求出a,c的值.
解答 解:(1)∵Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,且a:b=3:4,
∴设a=3x,则b=4x.
∵a2+b2=c2,即(3x)2+(4x)2=252,解得x=5,
∴a=3x=15,b=4x=20;
(2)∵△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c
∴a2+b2=c2,
∵c-a=4,b=12,
∴a2+144=(a+4)2,
解得:a=16,
∴c=20.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.甲、乙两名学生的十次数学竞赛训练成绩的平均分分别是115和116,成绩的方差分别是8.5和60.5,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
| A. | 甲、乙两人平均分相当,选谁都可以 | |
| B. | 乙的平均分比甲高,选乙 | |
| C. | 乙的平均分和方差都比甲高,成绩比甲稳定,选乙 | |
| D. | 两人的平均分相当,甲的方差小,成绩比乙稳定,选甲 |
6.关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}(2x+5)>x+1}\\{\frac{1}{2}(x+3)≤x+a}\end{array}\right.$只有5个整数解,则a的取值范围是( )
| A. | 3<a<$\frac{7}{2}$ | B. | 3≤a<$\frac{7}{2}$ | C. | 3<a≤$\frac{7}{2}$ | D. | 3≤a≤$\frac{7}{2}$ |
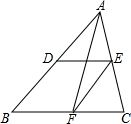 如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.
如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.