题目内容
5.若实数a,b,c满足a+b+c=0,且a<b<c,则一次函数y=ax+c的图象不可能经过第三象限.分析 根据实数a、b、c满足a+b+c=0,且a<b<c,确定a、c的取值范围,然后确定答案.
解答 解:∵实数a、b、c满足a+b+c=0,且a<b<c,
∴a<0,c>0,
∴一次函数y=ax+c的图象经过第一、二、四象限,不可能经过第三象限.
故答案为:三.
点评 本题考查了一次函数图象与系数的关系.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
相关题目
19. 如图,向阳中学七(6)班就上学方式作出调查后绘制了条形图,那么乘车上学的人数是( )
如图,向阳中学七(6)班就上学方式作出调查后绘制了条形图,那么乘车上学的人数是( )
 如图,向阳中学七(6)班就上学方式作出调查后绘制了条形图,那么乘车上学的人数是( )
如图,向阳中学七(6)班就上学方式作出调查后绘制了条形图,那么乘车上学的人数是( )| A. | 8 | B. | 16 | C. | 24 | D. | 48 |
17.先化简,再求值:a(a+b)(a-b)-a(a2-3b)+(a-b)2-a(a-b2),其中a=-2,b=$\sqrt{12}$-$\root{3}{8}$+($\frac{1}{2}$)-1.
15.反比例函数y=$\frac{k}{x}$(k<0),下列说法正确的是( )
| A. | 可以取任意实数 | B. | 函数图象在第一、三象限 | ||
| C. | 图象过点(1,k)和(-k,-1) | D. | 与函数y=4x的图象有两个交点 |
 如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2
如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2 如图,在△ABC中,∠C>∠B,AD是△ABC的角平分线,AE⊥BC于点E,试说明∠DAE=$\frac{1}{2}$(∠C-∠B).
如图,在△ABC中,∠C>∠B,AD是△ABC的角平分线,AE⊥BC于点E,试说明∠DAE=$\frac{1}{2}$(∠C-∠B). (1)∵∠A+∠B=180°(已知)
(1)∵∠A+∠B=180°(已知)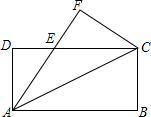 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E