题目内容
已知抛物线y=
x2-x-
(1)求该抛物线的对称轴和顶点坐标;
(2)求抛物线与x轴交点的坐标;
(3)画出抛物线的示意图,根据图象回答:当y>0时;写出x的取值范围.
| 1 |
| 2 |
| 3 |
| 2 |
(1)求该抛物线的对称轴和顶点坐标;
(2)求抛物线与x轴交点的坐标;
(3)画出抛物线的示意图,根据图象回答:当y>0时;写出x的取值范围.
考点:二次函数的性质,二次函数的图象
专题:
分析:(1)把抛物线解析式化为顶点式即可得出对称轴和顶点坐标;
(2)令y=0求得x的值,即可得出与x轴的交点坐标;
(3)利用描点法画出图象,当y>0时,即二次函数的图象在x轴上方的部分,找出对应的x的取值范围即可.
(2)令y=0求得x的值,即可得出与x轴的交点坐标;
(3)利用描点法画出图象,当y>0时,即二次函数的图象在x轴上方的部分,找出对应的x的取值范围即可.
解答:解:(1)∵y=
x2-x-
=
(x-1)2-2,
∴抛物线的对称轴为x=1,顶点坐标为(1,-2);
(2)令y=0可得
x2-x-
=0,解得x=-1或3,
∴抛物线与x轴的交点坐标为(-1,0)和(3,0);
(3)抛物线图象如图
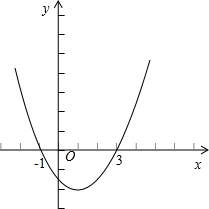
由图象可知当y>0时,x的取值范围为x<-1或x>3.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线的对称轴为x=1,顶点坐标为(1,-2);
(2)令y=0可得
| 1 |
| 2 |
| 3 |
| 2 |
∴抛物线与x轴的交点坐标为(-1,0)和(3,0);
(3)抛物线图象如图
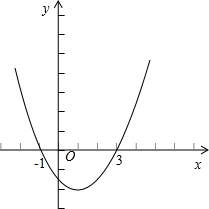
由图象可知当y>0时,x的取值范围为x<-1或x>3.
点评:本题主要考查二次函数的对称轴、顶点坐标及图象,掌握二次函数的顶点式y=a(x-h)2+k是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
如图,图中数轴的单位长度为1.如果点B,C表示的数的绝对值相等,那么点A与点D表示的数分别是( )

| A、-2,2 | B、-4,1 |
| C、-5,1 | D、-6,2 |
 如图,在△ABC中,CD⊥AB,垂足为D.下列条件:①∠A+∠B=90°;②AB2=AC2+BC2;③
如图,在△ABC中,CD⊥AB,垂足为D.下列条件:①∠A+∠B=90°;②AB2=AC2+BC2;③ 如图,M、N分别为AB、BC的中点,AC=8cm,求MN.
如图,M、N分别为AB、BC的中点,AC=8cm,求MN.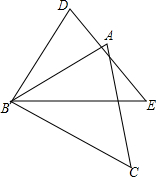 如图,AB=DB,∠CBE=∠ABD,请添加一个条件使△ABC≌△DBE,则需添加的条件是
如图,AB=DB,∠CBE=∠ABD,请添加一个条件使△ABC≌△DBE,则需添加的条件是