题目内容
已知二次函数y=-x2+4x.
(1)求函数图象的对称轴和顶点坐标;
(2)求这个函数图象与x轴的交点坐标.
(1)求函数图象的对称轴和顶点坐标;
(2)求这个函数图象与x轴的交点坐标.
考点:二次函数的性质
专题:
分析:(1)把二次函数化为顶点式,则可得出二次函数的对称轴和顶点坐标;
(2)令y=0,解得x的值,可得出函数图象与x轴的交点坐标.
(2)令y=0,解得x的值,可得出函数图象与x轴的交点坐标.
解答:解:(1)∵y=-x2+4x=-(x-2)2+4,
∴对称轴为x=2,顶点坐标为(2,4);
(2)令y=0得-x2+4x=0,解得x=0或4,
∴函数图象与x轴的交点坐标为(0,0)和(4,0).
∴对称轴为x=2,顶点坐标为(2,4);
(2)令y=0得-x2+4x=0,解得x=0或4,
∴函数图象与x轴的交点坐标为(0,0)和(4,0).
点评:本题主要考查二次函数的对称轴和顶点坐标,掌握二次函数的顶点式y=a(x-h)2+k是解题的关键.

练习册系列答案
相关题目
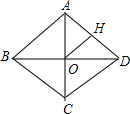 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )| A、4 | B、8 | C、16 | D、18 |
 如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )
如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )| A、AB=AC |
| B、BE=CD |
| C、角B=角C |
| D、角ADC=角AEB |
 如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长.
如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长. 如图,圆内接四边形ABCD中,∠A=62°,则∠C=
如图,圆内接四边形ABCD中,∠A=62°,则∠C=