题目内容
以(-3,4)为圆心,5为半径画圆,则圆与坐标轴交点坐标是 .
考点:垂径定理,坐标与图形性质,勾股定理
专题:计算题
分析:连结OP,作PC⊥OA于A,PD⊥OB于D,则OC=3,OD=4,根据勾股打开计算出OP=5,根据点与圆的位置关系判断点P在⊙P上,再根据垂径定理得到AC=OC=3,BD=OD=4,易得A(-6,0),B(0,8).
解答:解:如图,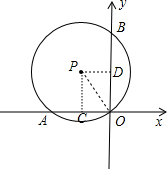 P(-3,4),
P(-3,4),
连结OP,作PC⊥OA于A,PD⊥OB于D,
则OC=3,OD=4,
∵OP=
=5,
而圆的半径为5,
∴点P在⊙P上,
∵PC⊥OA,PD⊥OB,
∴AC=OC=3,BD=OD=4,
∴A(-6,0),B(0,8),
即圆与坐标轴交点坐标为(0,0)、(0,8)、(-6,0).
故答案为(0,0)、(0,8)、(-6,0).
 P(-3,4),
P(-3,4),连结OP,作PC⊥OA于A,PD⊥OB于D,
则OC=3,OD=4,
∵OP=
| PC2+OC2 |
而圆的半径为5,
∴点P在⊙P上,
∵PC⊥OA,PD⊥OB,
∴AC=OC=3,BD=OD=4,
∴A(-6,0),B(0,8),
即圆与坐标轴交点坐标为(0,0)、(0,8)、(-6,0).
故答案为(0,0)、(0,8)、(-6,0).
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和坐标与图形性质.

练习册系列答案
相关题目
 如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA=
如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA= 如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长.
如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长. 如图,在矩形ABCD中,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,那么请求出此时BP的长.
如图,在矩形ABCD中,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,那么请求出此时BP的长. 已知△ABC(如图)
已知△ABC(如图) 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是27cm2,AB=10cm,AC=8cm,则DE的长为
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是27cm2,AB=10cm,AC=8cm,则DE的长为