题目内容
点P是△ABC内(不在边上)一点,连接PA、PB、PC,如果△PAB、△PBC、△PAC中存在一个三角形与原△ABC相似,那么我们把点P叫做△ABC的内相似点.已知在Rt△ABC中,∠ACB=90°,AC=3,BC=4,若点P是△ABC的内相似点,则cos∠PAB的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相似三角形的判定与性质
专题:新定义
分析:先找到Rt△ABC的内相似点,再根据三角函数的定义计算cos∠PAB即可.
解答: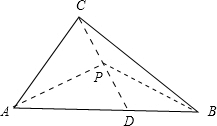 解:∵AC=3,BC=4,
解:∵AC=3,BC=4,
∴∠CAB>∠CBA,
故可在∠CAB内作∠CAP=∠CBA,
又∵点P为△ABC的内相似点,
∴过点C作CP⊥AP,并延长CP交AB于点D,
则△APC∽△BCA
∴点P为△ABC的内相似点,
∴∠ACP=∠CAB,
∴DA=DC,
在Rt△ABC中,AC=3,BC=4,则可求得AB=5,
由相似可知
=
,即
=
,解得AP=
,
在Rt△APC中,AC=3,AP=
,由勾股定理可求得PC=
,
设AD=x,则PD=x-
,且AP=
,由勾股定理可得AD2=AP2+PD2,
即x2=(
)2+(x-
)2,解得x=
,即AD=
,
∴cos∠PAB=
=
=
,
故选D.
 解:∵AC=3,BC=4,
解:∵AC=3,BC=4,∴∠CAB>∠CBA,
故可在∠CAB内作∠CAP=∠CBA,
又∵点P为△ABC的内相似点,
∴过点C作CP⊥AP,并延长CP交AB于点D,
则△APC∽△BCA
∴点P为△ABC的内相似点,
∴∠ACP=∠CAB,
∴DA=DC,
在Rt△ABC中,AC=3,BC=4,则可求得AB=5,
由相似可知
| AP |
| BC |
| AC |
| AB |
| AP |
| 4 |
| 3 |
| 5 |
| 12 |
| 5 |
在Rt△APC中,AC=3,AP=
| 12 |
| 5 |
| 9 |
| 5 |
设AD=x,则PD=x-
| 9 |
| 5 |
| 12 |
| 5 |
即x2=(
| 12 |
| 5 |
| 9 |
| 5 |
| 5 |
| 2 |
| 5 |
| 2 |
∴cos∠PAB=
| PA |
| AD |
| ||
|
| 24 |
| 25 |
故选D.
点评:本题主要考查相似三角形的判定和性质,利用条件先确定出P点的位置是解题的关键.

练习册系列答案
相关题目
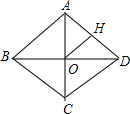 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )| A、4 | B、8 | C、16 | D、18 |
 如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA=
如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA= 如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长.
如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长. 已知△ABC(如图)
已知△ABC(如图)