题目内容
2.三角形的内心是三角形的( )| A. | 三条角平分线的交点 | B. | 三条中线的交点 | ||
| C. | 三条高的交点 | D. | 三边垂直平分线的交点 |
分析 根据三角形的内心的概念进行判断即可.
解答 解:三角形的内心就是三角形三个内角角平分线的交点.
故选:A.
点评 本题考查了三角形的内切圆与内心,与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,三角形的内心就是三角形三个内角角平分线的交点.记住三角形的内心到三角形三边的距离相等,三角形的内心与三角形顶点的连线平分这个内角是解题的关键.

练习册系列答案
相关题目
13.一个正多边形的每个外角都是60°,那么它是( )
| A. | 正六边形 | B. | 正七边形 | C. | 正八边形 | D. | 正九边形 |
7.在△ABC中,若∠A=∠B=$\frac{1}{2}$∠C,则∠C等于( )
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
12.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1、2、3、4、5,从中随机摸出一个小球,其标号小于3的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
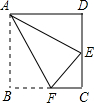 如图,将矩形ABCD沿AF折叠,点B落在CD边的中点E处,则图中等于60°的角(包括虚线)共有( )个.
如图,将矩形ABCD沿AF折叠,点B落在CD边的中点E处,则图中等于60°的角(包括虚线)共有( )个. 如图,点P是∠AOB的角平分线OC上任意一点,D、E点分别在射线OA、OB上,要使△POD≌△POE,还需添加一个条件,这个条件可以是OD=OE(写一种即可).
如图,点P是∠AOB的角平分线OC上任意一点,D、E点分别在射线OA、OB上,要使△POD≌△POE,还需添加一个条件,这个条件可以是OD=OE(写一种即可).
 如图,在宽为20m,长30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为504m2,则路宽为多少m?
如图,在宽为20m,长30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为504m2,则路宽为多少m?