题目内容
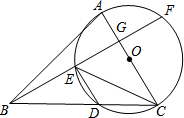 如图,在△ABC中,以AC为直径的⊙O交BC于点D,作BG⊥AC于点G,交⊙O于点E、F;
如图,在△ABC中,以AC为直径的⊙O交BC于点D,作BG⊥AC于点G,交⊙O于点E、F;(1)求证:∠EBC=∠DEC;
(2)若∠ABC=45°,⊙O的直径等于5,BD=4,求CG的长.
考点:圆周角定理,勾股定理
专题:计算题
分析:(1)证明:连接AD,如图,根据圆周角定理,由AC为直径得到∠ADC=90°,则∠CAD+∠ACD=90°,再由BG⊥AC得到∠EBC+∠ACD=90°,所以∠EBC=∠CAD,接着利用圆周角定理得∠CAD=∠DEC,于是有∠EBC=∠DEC;
(2)易得△ABD为等腰直角三角形,则AD=BD=4,在Rt△ADC中利用勾股定理计算出CD=3,则BC=BD+CD=7,再证明Rt△CBG∽Rt△CAD,然后利用相似比可计算出CE的长.
(2)易得△ABD为等腰直角三角形,则AD=BD=4,在Rt△ADC中利用勾股定理计算出CD=3,则BC=BD+CD=7,再证明Rt△CBG∽Rt△CAD,然后利用相似比可计算出CE的长.
解答: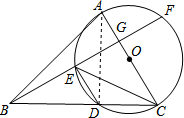 (1)证明:连接AD,如图,
(1)证明:连接AD,如图,
∵AC为直径,
∴∠ADC=90°,
∴∠CAD+∠ACD=90°,
∵BG⊥AC,
∴∠EBC+∠ACD=90°,
∴∠EBC=∠CAD,
∵∠CAD=∠DEC,
∴∠EBC=∠DEC;
(2)解:∵∠ADB=90°,∠ABC=45°,
∴△ABD为等腰直角三角形,
∴AD=BD=4,
在Rt△ADC中,∵AD=4,AC=5,
∴CD=
=3,
∴BC=BD+CD=7,
∵∠CBG=∠CAD,
∴Rt△CBG∽Rt△CAD,
∴CG:CD=CB:CA,即CG:3=7:5,
∴CG=
.
 (1)证明:连接AD,如图,
(1)证明:连接AD,如图,∵AC为直径,
∴∠ADC=90°,
∴∠CAD+∠ACD=90°,
∵BG⊥AC,
∴∠EBC+∠ACD=90°,
∴∠EBC=∠CAD,
∵∠CAD=∠DEC,
∴∠EBC=∠DEC;
(2)解:∵∠ADB=90°,∠ABC=45°,
∴△ABD为等腰直角三角形,
∴AD=BD=4,
在Rt△ADC中,∵AD=4,AC=5,
∴CD=
| AC2-AD2 |
∴BC=BD+CD=7,
∵∠CBG=∠CAD,
∴Rt△CBG∽Rt△CAD,
∴CG:CD=CB:CA,即CG:3=7:5,
∴CG=
| 21 |
| 5 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是( )
| A、点P在圆内 | B、点P在圆上 |
| C、点P在圆外 | D、不能确定 |
下列各式中,正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,∠B=90°,D在AC上,AD=AB=BC,DE⊥AC,垂足为D,求证:BE=DC.
如图,在△ABC中,∠B=90°,D在AC上,AD=AB=BC,DE⊥AC,垂足为D,求证:BE=DC.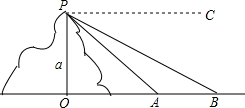 小强在山顶P处观测到有一河流,如图所示,设山的高度OP=a米,A、B分别是河两岸上的点,且A、B、O三点共线.从P点测得点A的俯角为α,点B的俯角为β,求河流的宽AB.
小强在山顶P处观测到有一河流,如图所示,设山的高度OP=a米,A、B分别是河两岸上的点,且A、B、O三点共线.从P点测得点A的俯角为α,点B的俯角为β,求河流的宽AB. 如图,已知双曲线y=
如图,已知双曲线y=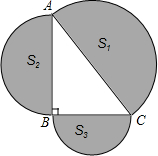 如图,在Rt△ABC中,∠ABC=90°,分别以AC、AB、BC为直径,在△ABC外作半圆,若S1=6,则S2+S3的值为
如图,在Rt△ABC中,∠ABC=90°,分别以AC、AB、BC为直径,在△ABC外作半圆,若S1=6,则S2+S3的值为