题目内容
如图，在锐角△ABC中，AD⊥BC，BC=AD=4，P是AB边上的一个动点，正方形PQRS是一个边长为x的动正方形，其中Q点在AC上，PQ∥BC，（RS与A分居PQ的两侧），正方形PQRS与△ABC的重叠的面积为y．
（1）当RS落在BC上时，求x的值；
（2）当RS不在BC上时，求y与x的关系式；
（3）求y的最大值．
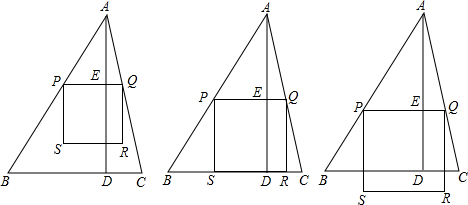
（1）当RS落在BC上时，求x的值；
（2）当RS不在BC上时，求y与x的关系式；
（3）求y的最大值．
考点：二次函数综合题,相似三角形的判定与性质
专题：
分析：（1）当RS落在BC上时，先求△ABC的BC边上的高，由△APQ∽△ABC，利用相似比求x；
（2）分两种情况，当0＜x＜2时，正方形面积即为公共部分面积；当2＜x≤4时，由相似得公共部分的长、宽，表示面积，
（3）根据所求函数关系式，结合自变量取值范围分别求最大值，比较得出结论．
（2）分两种情况，当0＜x＜2时，正方形面积即为公共部分面积；当2＜x≤4时，由相似得公共部分的长、宽，表示面积，
（3）根据所求函数关系式，结合自变量取值范围分别求最大值，比较得出结论．
解答：解：（1）∵PQ∥BC，
∴△APQ∽△ABC，
∴
=
，即
=
，
解得x=2；
（2）分两种情况：
ⅰ．当0＜x＜2时，y=x2；
ⅱ．当2＜x≤4时，
∵PQ∥BC，
∴△APQ∽△ABC，
∴
=
，即
=
，
解得AE=x，DE=4-x，
∴y=PQ•DE=x（4-x）=-x2+4x，
故y=
；
（3）①当RS落在△ABC外部时，y=-x2+4x=-（x-2）2+4（2＜x≤4），
∵当x=2时，y有最大值4，
∴y＜4；
②当RS落在BC边上时，由x=2可知，y=4，
③当RS落在△ABC内部时，y=x2＜4（0＜x＜2），
故比较以上三种情况可知：公共部分面积最大为4；
∴△APQ∽△ABC，
∴
| PQ |
| BC |
| AE |
| AD |
| x |
| 4 |
| 4-x |
| 4 |
解得x=2；
（2）分两种情况：
ⅰ．当0＜x＜2时，y=x2；
ⅱ．当2＜x≤4时，
∵PQ∥BC，
∴△APQ∽△ABC，
∴
| PQ |
| BC |
| AE |
| AD |
| x |
| 4 |
| AE |
| 4 |
解得AE=x，DE=4-x，
∴y=PQ•DE=x（4-x）=-x2+4x，
故y=
|
（3）①当RS落在△ABC外部时，y=-x2+4x=-（x-2）2+4（2＜x≤4），
∵当x=2时，y有最大值4，
∴y＜4；
②当RS落在BC边上时，由x=2可知，y=4，
③当RS落在△ABC内部时，y=x2＜4（0＜x＜2），
故比较以上三种情况可知：公共部分面积最大为4；
点评：本题考查了二次函数最值在求长方形面积中的运用．关键是根据题意表示长方形的面积，再根据自变量的取值范围及二次函数的最值求法求解．本题还考查了分类讨论的数学思想．
练习册系列答案
相关题目
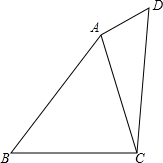已知：∠B=∠D，∠BCA+∠CAD=180°．求证：AB=CD．