题目内容
15.阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=$\frac{-1+2+3}{3}$=$\frac{4}{3}$;min{-1,2,3}=-1;min{-1,2,a}=$\left\{\begin{array}{l}{a(a≤-1)}\\{-1(a>-1)}\end{array}\right.$解决下列问题:
(1)min{ sin30°,tan45°,cos30°}$\frac{1}{2}$若min{2,2x+2,4-2x}=2,则x的范围为0≤x≤1;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么a=b=c(填a,b,c的大小关系)”.并证明你发现的结论;
③运用②的结论,填空:若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=4.
分析 (1)因为用min(a,b,c)表示这三个数中最小的数,由min{2,2x+2,4-2x}=2,得出2x+2≥2,且4-2x≥2,两个式子同时成立,据此即可求得x的范围;
(2)①M{2,x+1,2x}=x+1,若M{2,x+1,2x}=min{2,x+1,2x},则x+1是2、x+1、2x中最小的一个,即:x+1≤2且x+1≤2x,据此即可求得x的值;
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
解答 解:(1)min{ sin30°,tan45°,cos30°}=$\frac{1}{2}$;
由min{2,2x+2,4-2x}=2,得$\left\{\begin{array}{l}{2x+2≥2}\\{4-2x≥2}\end{array}\right.$,即0≤x≤1.
(2)①∵M{2,x+1,2x}=min{2,x+1,2x},
∴$\left\{\begin{array}{l}{x+1≤2x}\\{x+1≤2}\end{array}\right.$,即$\left\{\begin{array}{l}{x≥1}\\{x≤1}\end{array}\right.$,
∴x=1
②证明:由M{a,b,c}=min{a,b,c},可令$\frac{a+b+c}{3}$,即b+c=2a⑤;
又∵$\left\{\begin{array}{l}{\frac{a+b+c}{3}≤b}\\{\frac{a+b+c}{3}≤c}\end{array}\right.$,
解得:a+c≤2b ⑥,a+b≤2c⑦;
由⑤⑥可得c≤b;
由⑤⑦可得b≤c;
∴b=c;
将b=c代入⑤得c=a;
∴a=b=c.
③据②可得$\left\{\begin{array}{l}{2x+y+2=x+2y}\\{2x+y+2=2x-y}\end{array}\right.$,
解得y=-1,x=-3,
∴x+y=-4.
点评 本题考查一元一次不等式组的实际运用,解决的关键是读懂题意,根据题意结合方程和不等式去求解,综合运用知识解决问题.

 名校课堂系列答案
名校课堂系列答案 已知:菱形ABCD中,对角线AC与BD相交O.E是BC中点E,AD=6,则OE的长为( )
已知:菱形ABCD中,对角线AC与BD相交O.E是BC中点E,AD=6,则OE的长为( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{10}$ |
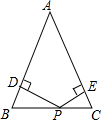 如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB,PE⊥AC,△ABC面积为4.
如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB,PE⊥AC,△ABC面积为4.


