题目内容
18.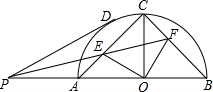 如图,PD为⊙O的切线,AB为⊙O的直径,OC⊥AB,PE为∠DPB的角平分线,交AC于E,交BC于F,求证:∠EOF=90°.
如图,PD为⊙O的切线,AB为⊙O的直径,OC⊥AB,PE为∠DPB的角平分线,交AC于E,交BC于F,求证:∠EOF=90°.
分析 如图,过C作CQ∥AB,交PF的延长线于Q,交PD的延长线于R,证得CQ是⊙O的切线,根据切线长定理得到RC=RD,根据平行线和角平分线得到∠Q=∠DPQ,证得DP=CQ,通过△CEQ∽△AEP,△CQF∽△BFP,得到$\frac{AE}{EC}=\frac{PA}{CQ}$,$\frac{CF}{FB}=\frac{CQ}{PB}$,根据切割线定理得到PD2=PA•PB,化为$\frac{PA}{CQ}=\frac{CQ}{PB}$,等量代换得到$\frac{AE}{CE}=\frac{CF}{FB}$,根据合比性质得$\frac{AE}{AC}=\frac{CF}{BC}$,推出△AEO≌△OCF,即可得到结论.
解答 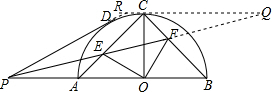 解:如图,过C作CQ∥AB,交PF的延长线于Q,交PD的延长线于R,
解:如图,过C作CQ∥AB,交PF的延长线于Q,交PD的延长线于R,
∵OC⊥AB,
∴CQ⊥OC,
∴CQ是⊙O的切线,
∴RC=RD,
∵CQ∥AB,
∴∠Q=∠DPQ,
∵∠DPQ=∠BPQ,
∴∠Q=∠DPQ,
∴DP=CQ,
∵CQ∥AB,
∴△CEQ∽△AEP,△CQF∽△BFP,
∴$\frac{AE}{EC}=\frac{PA}{CQ}$,$\frac{CF}{FB}=\frac{CQ}{PB}$,
∵PD2=PA•PB,
∴$\frac{PA}{CQ}=\frac{CQ}{PB}$,
∴$\frac{AE}{CE}=\frac{CF}{FB}$,
根据合比性质得$\frac{AE}{AC}=\frac{CF}{BC}$,
而AC=BC,
∴AE=CF,∠CAB=∠BCO=45°,
在△AEO与△OCF中$\left\{\begin{array}{l}{AE=CF}\\{∠EAO=∠FCO}\\{OA=OC}\end{array}\right.$,
∴△AEO≌△OCF,
∴∠AOE=∠COF,
∴∠AOE+∠EOC=∠FOC+∠EOC=90°,
∴∠EOF=90°.
点评 本题考查了切线的性质,相似三角形的判定和性质,全等三角形的判定和性质,角平分线的性质,正确的作出辅助线是解题的关键.

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案| A. | x-1 | B. | 2x | C. | 2x+1 | D. | x+1 |
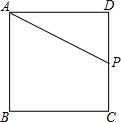 如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.
如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.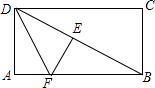 如图,折叠矩形纸片ABCD,得折痕BD,再折叠使AD边与对角线BD重合,得折痕DF.若AB=4,BC=2,则AF=$\sqrt{5}$-1.
如图,折叠矩形纸片ABCD,得折痕BD,再折叠使AD边与对角线BD重合,得折痕DF.若AB=4,BC=2,则AF=$\sqrt{5}$-1.