题目内容
8. 阅读下面一段对话,回答对话后面的问题:
阅读下面一段对话,回答对话后面的问题:在课外小组活动时,小慧拿来一道题(原问题)和小东交流.
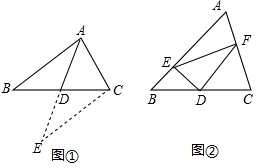
原问题:如图1,已知△ABC,D是BC的中点,求证:AB+AC>2AD
小慧同学的思路是:延长AD到E,使DE=AD,连接CE,易证△DCE≌△ABD,这样CE=AB,在△AEC中,由两边之和大于第三边,从而证明了不等式,这种构造辅助的方法是:借助过终点的线段,构造全等三角形,使问题得到了转化.
小东同学说:我做过一道类似的题目,也是证明一个不等式,我的题目如下“已知,如图②,△ABC中,D为BC中点,E为AB上一点,F为AC上一点,ED⊥DF,连接EF,求证:BE+FC>EF”,看来我可以类比你所展示的那道题目证明方法,作辅助线,从而证明出结论.
请你参考小慧同学的思路,探究并解决这提出的问题:
(1)请你完整证明出小慧同学所出的原问题.已知在△ABC中,D是BC中点,求证,AB+AC>2AD
(2)请你参考小慧同学的思路,帮小东同学完成证明过程:已知,如图②,△ABC中,D为BC中点,E为AB上一点,F为AC上一点,ED⊥DF,连接EF,求证:BE+FC>EF.
分析 (1)延长AD到E,使DE=AD,连接CE,易证△DCE≌△ABD,这样CE=AB,在△AEC中,由两边之和大于第三边,从而可证明结论;
(2)延长ED到G,使ED=DG,连接CG,FG,可证明△CGD≌△BED,可得CG=BE,在△CGF中由三角形三边关系可得CF|CG>FG,又可证明EF=FG,可证得结论.
解答 (1)证明:
如图①,延长AD到点E,使DE=AD,连接CE,
∵D为BC中点,
∴BD=CD,
在△ABD和△ECD中
$\left\{\begin{array}{l}{AD=DE}\\{∠ABD=∠CDE}\\{BD=CD}\end{array}\right.$
∴△ABD≌△ECD(SAS),
∴CE=AB,
在△ACE中,由三角形三边关系可得AC+CE>AE,
∴AB+AC>2AD;
(2)证明:
如图②,延长ED到G,使ED=DG,连接CG,FG,
∵D为BC的中点,
∴BD=DC,
在△BED和△CGD中
$\left\{\begin{array}{l}{BD=DC}\\{∠EDB=∠CDG}\\{DE=DG}\end{array}\right.$
∴△BED≌△CGD(SAS),
∴CG=BE,
在△CGF中,由三角形三边关系可得CF+CG>FG,
∴BE+CF>FG,
又ED⊥DF,
∴FD为EG的垂直平分线,
∴FG=EF,
∴BE+CF>EF.
点评 本题主要考查全等三角形的判定和性质,构造全等三角形,把线段转化成三角形的三边是解题的关键.

练习册系列答案
相关题目
19.边长为1的正方形的对角线长是( )
| A. | 整数 | B. | 分数 | C. | 有理数 | D. | 不是有理数 |
 如图,MN是线段AB的中垂线,MN=6,在MN上取C、D两点,连接AD,AC,BC,S△BMN:S△ADN=2:1,S△ADN:S△BCN=4:3,则CD的长度为$\frac{3}{4}$.
如图,MN是线段AB的中垂线,MN=6,在MN上取C、D两点,连接AD,AC,BC,S△BMN:S△ADN=2:1,S△ADN:S△BCN=4:3,则CD的长度为$\frac{3}{4}$.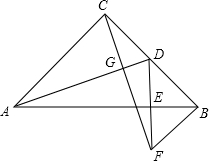 如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.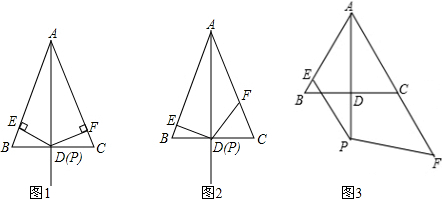
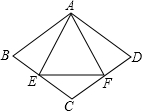 如图,在四边形ABCD中,AB=AD=BC=CD=4,AB∥CD,AD∥BC,∠BAD=120°.△AEF为等边三角形,点E,F分别在BC,CD上滑动,且点E,F不与点B,C,D重合,
如图,在四边形ABCD中,AB=AD=BC=CD=4,AB∥CD,AD∥BC,∠BAD=120°.△AEF为等边三角形,点E,F分别在BC,CD上滑动,且点E,F不与点B,C,D重合, 如图,△ABC中,∠B=90°,点M在AB上,AM=BC,作正方形CMDE,连接AD.
如图,△ABC中,∠B=90°,点M在AB上,AM=BC,作正方形CMDE,连接AD.