题目内容
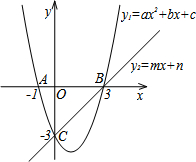 如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.
如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.(1)抛物线y1=ax2+bx+c的解析式为
(2)当x满足
(3)当x满足
(4)当x满足
考点:二次函数与不等式(组)
专题:
分析:(1)设抛物线y1=a(x+1)(x-3),将点C(0,-3)代入,得到关于a的方程,解方程求出a的值,进而得到抛物线y1=ax2+bx+c的解析式;
(2)抛物线y1在x轴下方的部分对应的x的取值即为所求;
(3)抛物线y1在直线y2上方的部分对应的x的取值即为所求;
(4)当y1与y2同在x轴下方或同在x轴上方时对应的x的取值即为所求.
(2)抛物线y1在x轴下方的部分对应的x的取值即为所求;
(3)抛物线y1在直线y2上方的部分对应的x的取值即为所求;
(4)当y1与y2同在x轴下方或同在x轴上方时对应的x的取值即为所求.
解答:解:(1)设抛物线y1=a(x+1)(x-3),
将点C(0,-3)代入,得-3=-3a,
解得a=1,
所以y1=(x+1)(x-3)=x2-2x-3,
即抛物线y1=ax2+bx+c的解析式为y1=x2-2x-3;
(2)由图象可知,当-1<x<3时,ax2+bx+c<0;
(3)由图象可知,当x<0或x>3时,y1>y2;
(4)由图象可知,当-1<x<0或x>3时,y1•y2>0.
故答案为y1=x2-2x-3;-1<x<3;x<0或x>3;-1<x<0或x>3.
将点C(0,-3)代入,得-3=-3a,
解得a=1,
所以y1=(x+1)(x-3)=x2-2x-3,
即抛物线y1=ax2+bx+c的解析式为y1=x2-2x-3;
(2)由图象可知,当-1<x<3时,ax2+bx+c<0;
(3)由图象可知,当x<0或x>3时,y1>y2;
(4)由图象可知,当-1<x<0或x>3时,y1•y2>0.
故答案为y1=x2-2x-3;-1<x<3;x<0或x>3;-1<x<0或x>3.
点评:本题考查了二次函数与不等式(组),待定系数法求二次函数的解析式,利用数形结合是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
下列各式中的大小关系成立的是( )
| A、-π>-3.14 | ||
| B、-23>-32 | ||
C、-
| ||
| D、-|-3|>-2 |
下列从左到右的变形,属因式分解的有( )
| A、(x+a)(x-a)=x2-a2 | ||
| B、x2-4x+3=x(x-4)+3 | ||
| C、x3-8x2=x2(x-8) | ||
D、x+y=x(1+
|
下列长度的三条线段,能首尾相接构成三角形的是( )
| A、1cm,2cm,3cm |
| B、3cm,3cm,3cm. |
| C、2cm,5cm,8cm |
| D、1.3cm,1.2cm,2.5cm |
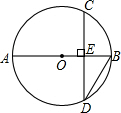 如图,AB为⊙O的直径,弦CD⊥AB于E,已知AB=20,EB=2,求CD的长.
如图,AB为⊙O的直径,弦CD⊥AB于E,已知AB=20,EB=2,求CD的长.