题目内容
12.已知二次函数的图象的顶点在原点O,且经过点A(1,$\frac{1}{4}$).(1)求此函数的解析式;
(2)将该抛物线沿着y轴向上平移后顶点落在点P处,直线x=2分别交原抛物和新抛物线于点M和N,且S△PMN=$3\sqrt{2}$,求:MN的长以及平移后抛物线的解析式.
分析 (1)根据题意可直接设y=ax2把点(1,-3)代入得a=-3,所以y=-3x2;
(2)设平移后y=$\frac{1}{4}$x2+d(d>0),则MN=d,根据题意得出S=$\frac{1}{2}$×2×d=3$\sqrt{2}$,即可求得d的值,从而求得平移后的解析式.
解答 解:(1)∵抛物线顶点是原点,可设y=ax2,
把点A(1,$\frac{1}{4}$)代入,得a=,$\frac{1}{4}$,
所以这个二次函数的关系式为y=$\frac{1}{4}$x2;
(2)设平移后y=$\frac{1}{4}$x2+d(d>0),
∴MN=d,S=$\frac{1}{2}$×2×d=3$\sqrt{2}$,
∴d=3$\sqrt{2}$,
∴y=$\frac{1}{4}$x2+3$\sqrt{2}$.
点评 主要考查了用待定系数法求函数解析式以及二次函数的图象与几何变换,熟练掌握待定系数法和平移的规律是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.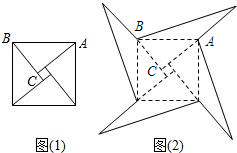 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 76 | B. | 72 | C. | 68 | D. | 52 |
20.下列说法正确的是( )
| A. | 1的平方根是1 | B. | 1是算术平方根是±1 | ||
| C. | -1的立方根是-1 | D. | (-1)2的平方根是-1 |
17.一个等腰三角形的两边分别为4cm和10cm,则该等腰三角形的周长为(单位:cm)( )
| A. | 14 | B. | 18 | C. | 24 | D. | 18或24 |
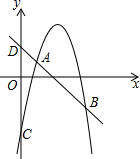 已知:抛物线y=-x2+bx+c的图象交y轴于点C,一次函数y=-x+m交y轴于点D,交抛物线于A、B两点,B(6,-3),且AB=2AD.
已知:抛物线y=-x2+bx+c的图象交y轴于点C,一次函数y=-x+m交y轴于点D,交抛物线于A、B两点,B(6,-3),且AB=2AD. 若一次函数y=kx+4的图象经过点(1,2).
若一次函数y=kx+4的图象经过点(1,2).