题目内容
 如图,矩形OABC的顶点A,C分别在x轴和y上,点B的坐标为(-2,3),双曲线y=
如图,矩形OABC的顶点A,C分别在x轴和y上,点B的坐标为(-2,3),双曲线y=| k |
| x |
(1)求k的值及点E的坐标.
(2)若点F是OC边上一点,且∠BDE=∠CFB,求直线FB的解析式.
考点:反比例函数综合题
专题:
分析:(1)利用待定系数法即可求得k的值,得到解析式,然后代入点E的横坐标,即可求得E点的坐标;
(2)先求得△FBC∽△DEB,得出CF的长,进而得出OF的坐标,然后应用待定系数法即可求得直线FB的解析式;
(2)先求得△FBC∽△DEB,得出CF的长,进而得出OF的坐标,然后应用待定系数法即可求得直线FB的解析式;
解答: 解:(1)∵点B的坐标是(-2,3),
解:(1)∵点B的坐标是(-2,3),
∴中点D的坐标是(-1,3),
∵y=
(k<0)经过点D,
∴3=
,解得k=-3,
∵点E在AB 上,
∴点E的横坐标是-2,
∵y=
经过点E,
∴点E的纵坐标是
,
∴点E的坐标是(-2,
);
(2)由(1)得,BD=1,BE=
,BC=2,
∵∠BDE=∠CFB,∠DBE=∠FCB=90°,
∴△FBC∽△DEB,
∴
=
,即
=
,
∴CF=
,
∴OF=
,即点F的坐标是(0,
),
设直线FB的解析式为:y=k1x+b,
则
解得
,
∴直线FB的解析式为:y=-
x+
.
 解:(1)∵点B的坐标是(-2,3),
解:(1)∵点B的坐标是(-2,3),∴中点D的坐标是(-1,3),
∵y=
| k |
| x |
∴3=
| k |
| -1 |
∵点E在AB 上,
∴点E的横坐标是-2,
∵y=
| -3 |
| x |
∴点E的纵坐标是
| 3 |
| 2 |
∴点E的坐标是(-2,
| 3 |
| 2 |
(2)由(1)得,BD=1,BE=
| 3 |
| 2 |
∵∠BDE=∠CFB,∠DBE=∠FCB=90°,
∴△FBC∽△DEB,
∴
| BD |
| CF |
| BE |
| CB |
| 1 |
| CF |
| ||
| 2 |
∴CF=
| 4 |
| 3 |
∴OF=
| 5 |
| 3 |
| 5 |
| 3 |
设直线FB的解析式为:y=k1x+b,
则
|
|
∴直线FB的解析式为:y=-
| 2 |
| 3 |
| 5 |
| 3 |
点评:本题考查了待定系数法求解析式的方法的应用,三角形相似的判定及性质等.

练习册系列答案
相关题目
在平面坐标系中,线段AB的两端点的坐标分别是A(-1,2)、B(-2,3),若线段AB平移后的点B的坐标为(1,4),则平移后点A的坐标是( )
| A、(2,3) |
| B、(-2,-3) |
| C、(2,-3) |
| D、(-2,3). |
 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.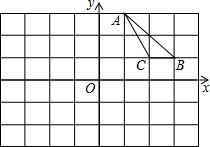 如图,平面直角坐标系中,△ABC的三个顶点A(1,3),B(3,1),C(2,1)
如图,平面直角坐标系中,△ABC的三个顶点A(1,3),B(3,1),C(2,1) 今年“六一”儿童节当天,小兵一家三口自驾车去离家220千米的“儿童乐园”游玩,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
今年“六一”儿童节当天,小兵一家三口自驾车去离家220千米的“儿童乐园”游玩,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. 如图,已知DE∥BC,BE平分∠ABNC,∠C=55°,∠ABC=70°.
如图,已知DE∥BC,BE平分∠ABNC,∠C=55°,∠ABC=70°.
