题目内容
4.下列各组式子中,不是同类二次根式的是( )| A. | $\sqrt{\frac{1}{8}}$和$\sqrt{18}$ | B. | $\sqrt{63}$和$\sqrt{\frac{25}{28}}$ | C. | $\sqrt{48}$和$\sqrt{4.8}$ | D. | $\sqrt{0.125}$和$\sqrt{128}$ |
分析 根据同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式,可得答案.
解答 解:A、$\sqrt{\frac{1}{8}}$=$\frac{\sqrt{2}}{4}$,$\sqrt{18}$=3$\sqrt{2}$,故A是同类二次根式;
B、$\sqrt{63}$=3$\sqrt{7}$,$\sqrt{\frac{25}{28}}$=$\frac{5\sqrt{7}}{14}$,故B是同类项二次根式;
C、$\sqrt{48}$=4$\sqrt{3}$,$\sqrt{4.8}$=$\frac{2\sqrt{30}}{5}$,不是同类二次根式,故C正确;
D、$\sqrt{0.125}$=$\frac{\sqrt{2}}{4}$,$\sqrt{128}$=8$\sqrt{2}$,故D是同类二次根式;
故选:C.
点评 本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
12.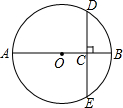 如图,⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,则弦DE的长为( )
如图,⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,则弦DE的长为( )
 如图,⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,则弦DE的长为( )
如图,⊙O的直径AB=8,弦DE经过OB的中点C且DE⊥OB,则弦DE的长为( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
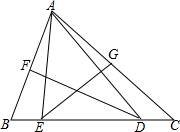 如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数.
如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数. 如图,△ABC中,BC的垂直平分线交AB于点D,交BC于点E,若AB=6,AC=4,求△ACD的周长.
如图,△ABC中,BC的垂直平分线交AB于点D,交BC于点E,若AB=6,AC=4,求△ACD的周长.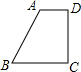 将如图所示的直角梯形绕直角边CD旋转一周,所得几何体的主视图是( )
将如图所示的直角梯形绕直角边CD旋转一周,所得几何体的主视图是( )