题目内容
1．下列说法错误的是（ ）| A． | 有两个角互余的三角形一定是直角三角形 | |
| B． | 直角三角形中，若一直角边等于斜边的一半，则这条直角边所对的角为30° | |
| C． | 直角三角形斜边上的中线等于斜边的一半 | |
| D． | △ABC中，若∠A：∠B：∠C=1：3：5，则这个三角形为直角三角形 |
分析 根据三角形内角和和三角形得分类对A、D进行判断；根据含30度的直角三角形三边的关系对B进行判断；根据直角三角形斜边上的中线性质对C进行判断．
解答 解：A、有两个角互余的三角形一定是直角三角形，所以A选项的说法正确；
B、直角三角形中，若一直角边等于斜边的一半，则这条直角边所对的角为30°，所以B选项的说法正确；
C、直角三角形斜边上的中线等于斜边的一半，所以C选项的说法正确；
D、△ABC中，若∠A：∠B：∠C=1：3：5，则∠C=$\frac{5}{9}$×180°=100°，所以这个三角形为钝角三角，所以D选项的说法错误．
故选D．
点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式． 2、有些命题的正确性是用推理证实的，这样的真命题叫做定理．
练习册系列答案
名校课堂系列答案
相关题目
12．
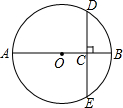如图，⊙O的直径AB=8，弦DE经过OB的中点C且DE⊥OB，则弦DE的长为（ ）
如图，⊙O的直径AB=8，弦DE经过OB的中点C且DE⊥OB，则弦DE的长为（ ）| A． | 3$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 6$\sqrt{3}$ |
如图，△ABC中，BC的垂直平分线交AB于点D，交BC于点E，若AB=6，AC=4，求△ACD的周长．
6．
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | 3$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
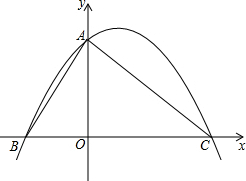将直角边长为4的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B（-2，0）． 
如图所示的几何体是由7个相同的正方体搭成的，请画出它的主视图、左视图和俯视图．