题目内容
4.在等腰△ABC中(AB=AC≠BC),在△ABC所在一平面内找一点P,使得△PAB,△PAC,△PBC都是等腰三角形,则满足此条件的点有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据等腰三角形的判定,“在同一三角形中,有两条边相等的三角形是等腰三角形(简称:在同一三角形中,等边对等角)”解答即可.
解答 解:①作三边的垂直平分线必在三角形内交于一点,这点就是符合要求的P点,
②作BC的垂直平分线,以B点为圆心画弧交BC的垂直平分线另一点,这点也是符合要求的P点
③作BC的垂直平分线,以A点为圆心画弧交BC的垂直平分线一点,这点也是符合要求的P点
④在△ABC的右边作一个△APB,使△APB≌△ABC,这点也是符合要求的P点
故选D
点评 本题考查了等腰三角形的判定;构造等腰三角形时本着截取相同的线段就能作出等腰三角形来.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.以下变换可以改变图形的大小的是( )
| A. | 位似变换 | B. | 旋转变换 | C. | 轴对称变换 | D. | 平移变换 |
 如图所示,AB∥CD,∠1=∠4,求证:EG∥FH.
如图所示,AB∥CD,∠1=∠4,求证:EG∥FH. A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,l1,l2分别表示两辆汽车的s与t的关系.
A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,l1,l2分别表示两辆汽车的s与t的关系.
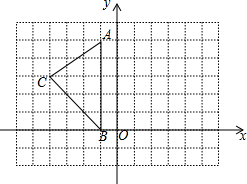 如图,在平面直角坐标系中,已知三点A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,已知三点A(-1,5),B(-1,0),C(-4,3). 如图所示,在道路OA、OB的交叉区域内有M、N两所学校,现要在此区域内建一图书馆P,使它到两条道路的距离相等,并且到两所学校的距离也相等,求P点位置.(不写作法,保留作图痕迹)
如图所示,在道路OA、OB的交叉区域内有M、N两所学校,现要在此区域内建一图书馆P,使它到两条道路的距离相等,并且到两所学校的距离也相等,求P点位置.(不写作法,保留作图痕迹)