题目内容
 如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,求MD的长.
如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,求MD的长.考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:延长BD交AC于点N,通过证明全等三角形得到D点是BN的中点,然后求出CN的长,利用三角形中位线定理求得DM的长即可.
解答: 解:延长BD交AC于点N.
解:延长BD交AC于点N.
∵BD⊥AD,AD平分∠BAC,
∴∠ADB=∠ADN=90°,∠BAD=∠NAD.
在△ABD与△AND中,
,
∴△ABD≌△AND (角边角),
∴BD=DN,AB=AN=12,
∴CN=AC-AN=10,
又∵BM=MC,
∴DM=
CN=5.
 解:延长BD交AC于点N.
解:延长BD交AC于点N.∵BD⊥AD,AD平分∠BAC,
∴∠ADB=∠ADN=90°,∠BAD=∠NAD.
在△ABD与△AND中,
|
∴△ABD≌△AND (角边角),
∴BD=DN,AB=AN=12,
∴CN=AC-AN=10,
又∵BM=MC,
∴DM=
| 1 |
| 2 |
点评:本题考查了三角形的中位线定理,通过证明得到中点,进而得到三角形的中位线,利用中位线定理求得即可.

练习册系列答案
相关题目

 如图,在△ABC中,∠B=40°,∠C=110°.
如图,在△ABC中,∠B=40°,∠C=110°. 在平面直角坐标系中,
在平面直角坐标系中,
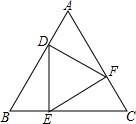 如图,△ABC是边长为6的等边三角形,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,则AD=
如图,△ABC是边长为6的等边三角形,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,则AD=