题目内容
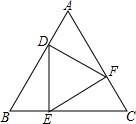 如图,△ABC是边长为6的等边三角形,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,则AD=
如图,△ABC是边长为6的等边三角形,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,则AD=考点:等边三角形的性质
专题:
分析:先由△ABC是等边三角形求得△DEF为等边三角形,再利用,△ADF≌△DEB≌△EFC,和勾股定理即可求出答案.
解答:解:由△ABC是等边三角形得,∠ABC=∠ACB=∠BAC=60°
又∵DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,
∴∠EDF=∠EFD=∠DEF=60°,
∴△DEF为等边三角形,
∴△ADF≌△DEB≌△EFC,
∴AD=BE=CF,
∵FD⊥AB,∠AFD=30°,
∴AD=
=
,
∴AD=
,
解得:AD=2.
故答案为:2.
又∵DE⊥BC于E,EF⊥AC于F,FD⊥AB于D,
∴∠EDF=∠EFD=∠DEF=60°,
∴△DEF为等边三角形,
∴△ADF≌△DEB≌△EFC,
∴AD=BE=CF,
∵FD⊥AB,∠AFD=30°,
∴AD=
| AF |
| 2 |
| AC-CF |
| 2 |
∴AD=
| 6-AD |
| 2 |
解得:AD=2.
故答案为:2.
点评:此题考查了等腰三角形的判定与性质和等边三角形的性质的理解和掌握,还涉及到直角三角形的特点,此题的关键是先求证△DEF为等边三角形,然后利用勾股定理求得的.

练习册系列答案
相关题目
下列方程中,解为x=4的是( )
| A、2x+1=10 | ||
| B、-3x-8=5 | ||
C、
| ||
| D、2(x-1)=6 |
 如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,求MD的长.
如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,求MD的长. 如图,在矩形ABCD中,AB=2,AD=5,点P在线段BC上运动,现将纸片折叠,使点A与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),设BP=x,当点E落在线段AB上,点F落在线段AD上时,x的取值范围是
如图,在矩形ABCD中,AB=2,AD=5,点P在线段BC上运动,现将纸片折叠,使点A与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),设BP=x,当点E落在线段AB上,点F落在线段AD上时,x的取值范围是 如图,在?ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为
如图,在?ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为