题目内容
3.设二次方程ax2+bx+c=0的系数a、b、c都是奇数,它的两个实根x1、x2满足-1<x1<0,x2>1,若b2-4ac=5,求x1、x2.分析 根据二次方程ax2+bx+c=0的系数a、b、c都是奇数,它的两个实根x1、x2满足-1<x1<0,x2>1,若b2-4ac=5,根与系数的关系,可以得到a、c的值以及a、c与b的关系,从而可以得到x1、x2的值.
解答 解:∵二次方程ax2+bx+c=0的系数a、b、c都是奇数,它的两个实根x1、x2满足-1<x1<0,x2>1,b2-4ac=5,
∴${x}_{1}{x}_{2}=\frac{c}{a}<0$,b2=5+4ac>0,
∴$ac>-\frac{4}{5}$,
∴$-\frac{4}{5}<ac<0$,
∴当a=1时,c=-1或a=-1时,c=1;
∴当a=1时,c=-1时,$\left\{\begin{array}{l}{{x}_{1}{x}_{2}=\frac{c}{a}=\frac{-1}{1}=-1}\\{{x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{b}{1}}\\{{b}^{2}-4ac={b}^{2}-4×1×(-1)={b}^{2}+4=5}\end{array}\right.$
解得$x=\frac{-1±\sqrt{5}}{2}$或x=$\frac{1±\sqrt{5}}{2}$,
∵-1<x1<0,x2>1,
∴${x}_{1}=\frac{1-\sqrt{5}}{2},{x}_{2}=\frac{1+\sqrt{5}}{2}$,
当a=-1,c=1时,$\left\{\begin{array}{l}{{x}_{1}{x}_{2}=\frac{c}{a}=\frac{1}{-1}=-1}\\{{x}_{1}+{x}_{2}=-\frac{b}{a}=-\frac{b}{-1}=b}\\{{b}^{2}-4ac={b}^{2}-4×(-1)×1={b}^{2}+4=5}\end{array}\right.$
解得$x=\frac{-1±\sqrt{5}}{2}$或x=$\frac{1±\sqrt{5}}{2}$,
∵-1<x1<0,x2>1,
∴${x}_{1}=\frac{1-\sqrt{5}}{2},{x}_{2}=\frac{1+\sqrt{5}}{2}$,
由上可得,${x}_{1}=\frac{1-\sqrt{5}}{2},{x}_{2}=\frac{1+\sqrt{5}}{2}$.
点评 本题考查根与系数的关系、不等式,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.

| A. | 22015 | B. | 22014 | C. | -22014 | D. | 3×22014 |
| A. | y=$\frac{1}{2}$x2 | B. | y=(x+0.5)2+2 | C. | y=(x-0.5)2+2 | D. | y=x2-2x-0.5 |
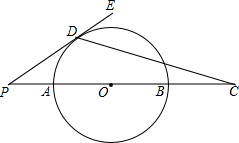 如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )
如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{13}}{13}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{13}}{13}$ |
| A. | 2是不等式x-3<8的解 | B. | -4不是不等式$\frac{1}{2}$x+2>0的解 | ||
| C. | -1是不等x≥-2的解 | D. | 不等式x>0和x≥0的解集相同 |
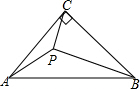 如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.
如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.